Comprendre les variations avec la dérivée
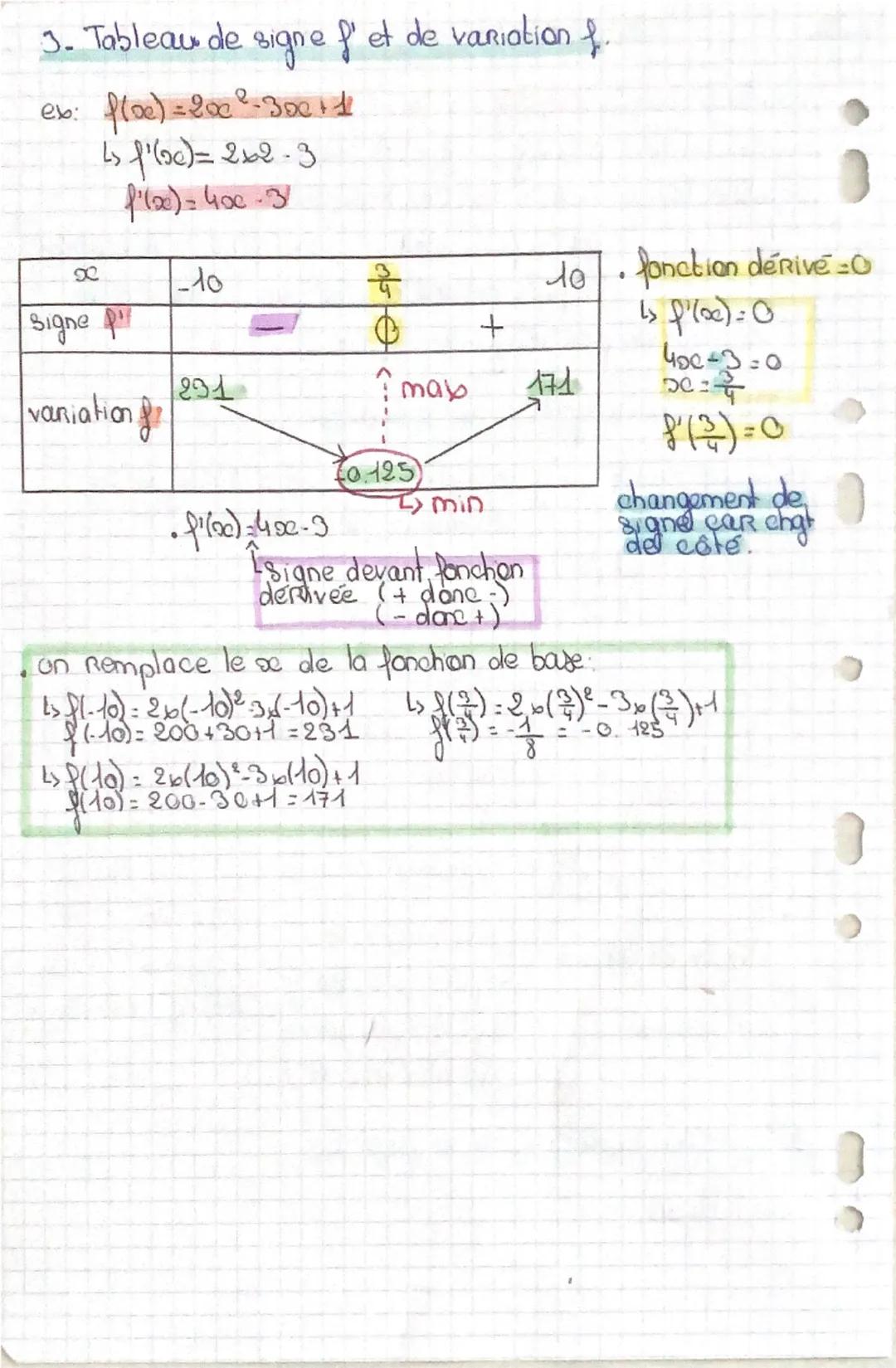
Tu sais déjà que la dérivée te donne la pente d'une courbe, mais voici ce qui va te sauver aux contrôles : quand f'(x) est positive, ta fonction monte. Quand f'(x) est négative, elle descend.
Le truc magique ? Quand f'(x) = 0, ta fonction passe par un point horizontal - c'est là que tu trouves tes minimums et maximums. Si la fonction descend puis remonte, tu as un minimum. Si elle monte puis redescend, c'est un maximum.
Pour placer une tangente, choisis un point d'abscisse parexemplex=3, calcule f(3) pour l'ordonnée, puis f'(3) pour la pente. Ta tangente a pour équation y = f'(3)x + b, et elle passe par le point (3, f(3)).
Astuce pratique : Fais toujours un tableau de valeurs avec quelques points pour visualiser le comportement de ta fonction !