Bornes et convergence des suites
Tu galères avec les suites qui semblent partir dans tous les sens ? Pas de panique, il existe des moyens simples de les "encadrer" et prédire leur comportement !
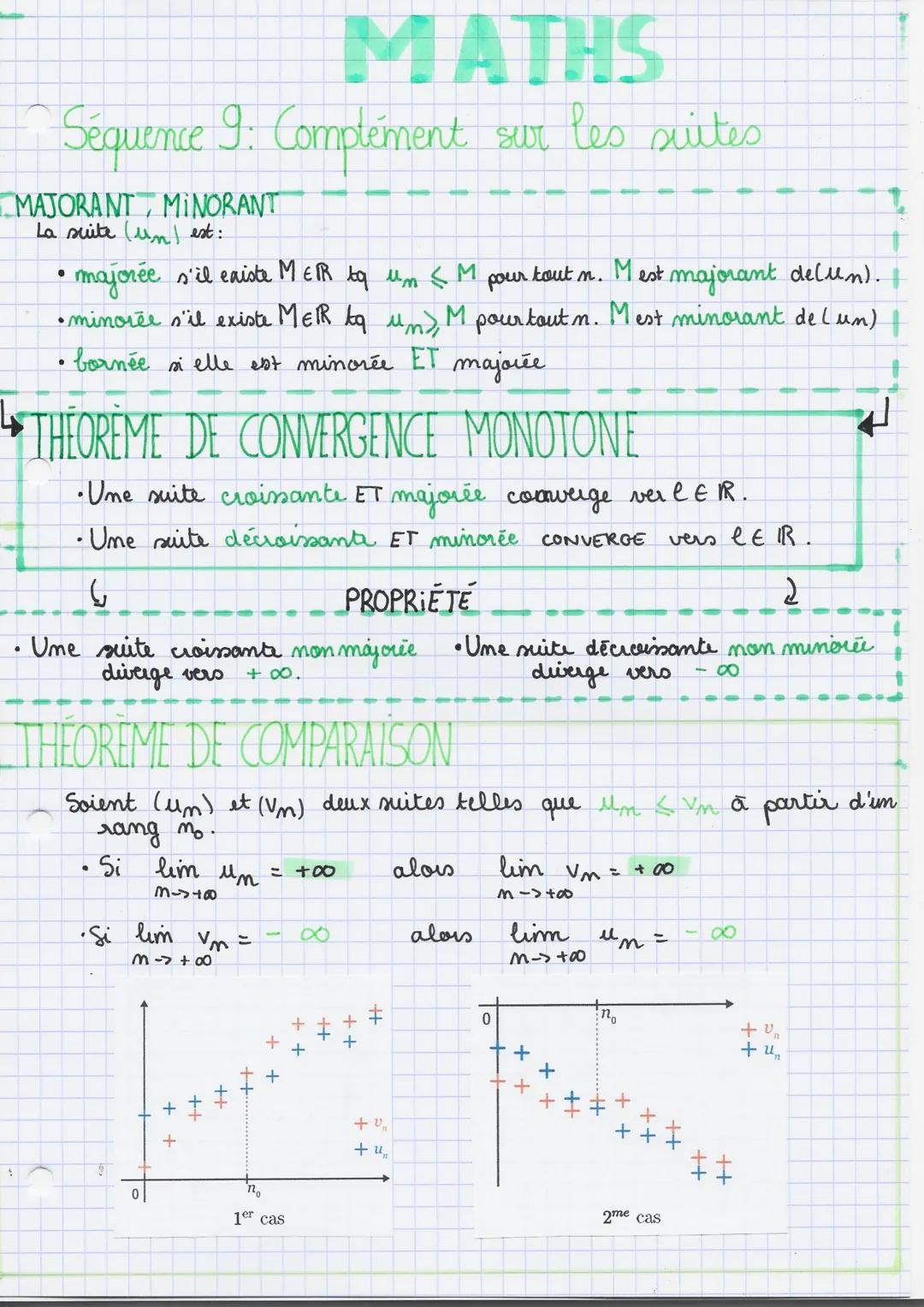
Une suite majorée reste toujours sous une certaine valeur M (comme un plafond qu'elle ne peut pas dépasser). À l'inverse, une suite minorée ne descend jamais en dessous d'une valeur m. Quand une suite est à la fois majorée ET minorée, elle est bornée - elle évolue dans un "couloir" bien défini.
Le théorème de convergence monotone est ton meilleur ami : une suite croissante et majorée converge forcément, tout comme une suite décroissante et minorée. C'est logique : si elle monte mais ne peut pas dépasser un plafond, elle finit par se stabiliser !
Le théorème de comparaison permet de comparer deux suites. Si u_n ≤ v_n et que u_n tend vers +∞, alors v_n aussi. C'est comme dire : si le plus petit explose, le plus grand aussi !
Astuce : Pour montrer qu'une suite converge, cherche d'abord si elle est monotone, puis trouve ses bornes !