Tangente et formules de base

Tu veux tracer la tangente à une courbe en un point ? C'est parti ! La formule de la tangente au point A est : y = g'$a$ × $x-a$ + g$a$.

Voici les formules de dérivation essentielles à retenir. Pour une constante g$x$ = k, la dérivée g'$x$ = 0. Pour une fonction affine g$x$ = ax + b, on obtient g'$x$ = a.

Les puissances suivent une règle simple : g$x$ = x^n donne g'$x$ = nx^$n-1$. Par exemple, x² devient 2x, et x³ devient 3x². Pour les cas particuliers : 1/x donne -1/x², e^x reste e^x, et √x devient 1/(2√x).

Astuce : La dérivée te donne le coefficient directeur de la tangente !

Opérations et fonctions composées

Les opérations sur les dérivées sont ton meilleur ami pour les calculs complexes. Addition : $u+v$' = u' + v'. Multiplication par une constante : (ku)' = ku'.

Pour le produit, retiens la formule : (uv)' = u'v + uv'. Le quotient suit : (u/v)' = $u'v - uv'$/v².

Les fonctions composées demandent plus d'attention. Pour f(g$x$), utilise : f'(g$x$) × g'$x$. Pour f$ax+b$, c'est f'$ax+b$ × a. L'exponentielle composée e^(g$x$) donne e^(g$x$) × g'$x$.

Les tableaux de variation pour les fonctions affines dépendent du signe de a. Si a > 0, la fonction est croissante ; si a < 0, elle est décroissante.

Important : Pour les fonctions composées, n'oublie jamais de multiplier par la dérivée de la fonction "intérieure" !

Polynômes du second degré

Les paraboles (ax²) ont un comportement qui dépend du signe de a. Si a > 0, elle forme un U ; si a < 0, elle forme un ∩.

Pour créer ton tableau de variation, calcule d'abord le discriminant : Δ = b² - 4ac. Ce nombre magique détermine tout !

Si Δ > 0, tu as deux racines : x₁ = $-b - √Δ$/(2a) et x₂ = $-b + √Δ$/(2a). Ton tableau aura alors trois colonnes avec les signes qui changent à chaque racine.

Le sens de variation dépend du signe de a. La dérivée change de signe aux racines, ce qui crée les points où la fonction passe de croissante à décroissante (ou vice versa).

Méthode : Commence toujours par calculer Δ - ça détermine la forme de ton tableau !

Cas particuliers du discriminant

Quand Δ < 0, pas de racine réelle ! Ton tableau de variation est simple : la dérivée garde le même signe sur tout ℝ.

Si a > 0, la fonction est toujours décroissante puis croissante. Si a < 0, c'est l'inverse. Le tableau n'a qu'une seule "zone" de chaque côté.

Pour Δ = 0, tu obtiens une racine double : x₀ = -b/(2a). C'est le sommet de ta parabole ! Ton tableau ressemble au cas Δ < 0, mais avec un point particulier où la dérivée s'annule.

Les fonctions avec racines carrées nécessitent une étape supplémentaire. Avant de dériver √$ax+b$, pose l'inéquation ax+b ≥ 0 pour trouver le domaine de définition.

Attention : N'oublie jamais de vérifier le domaine de définition avant de dériver !

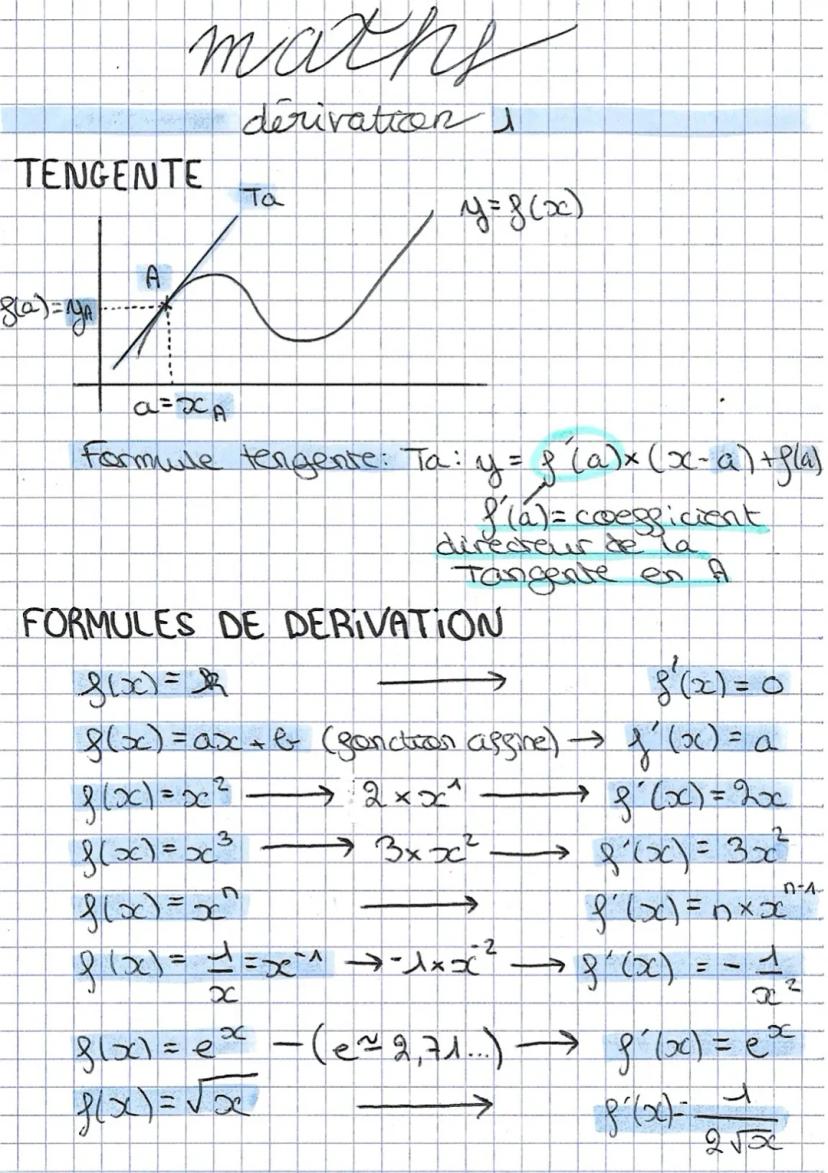
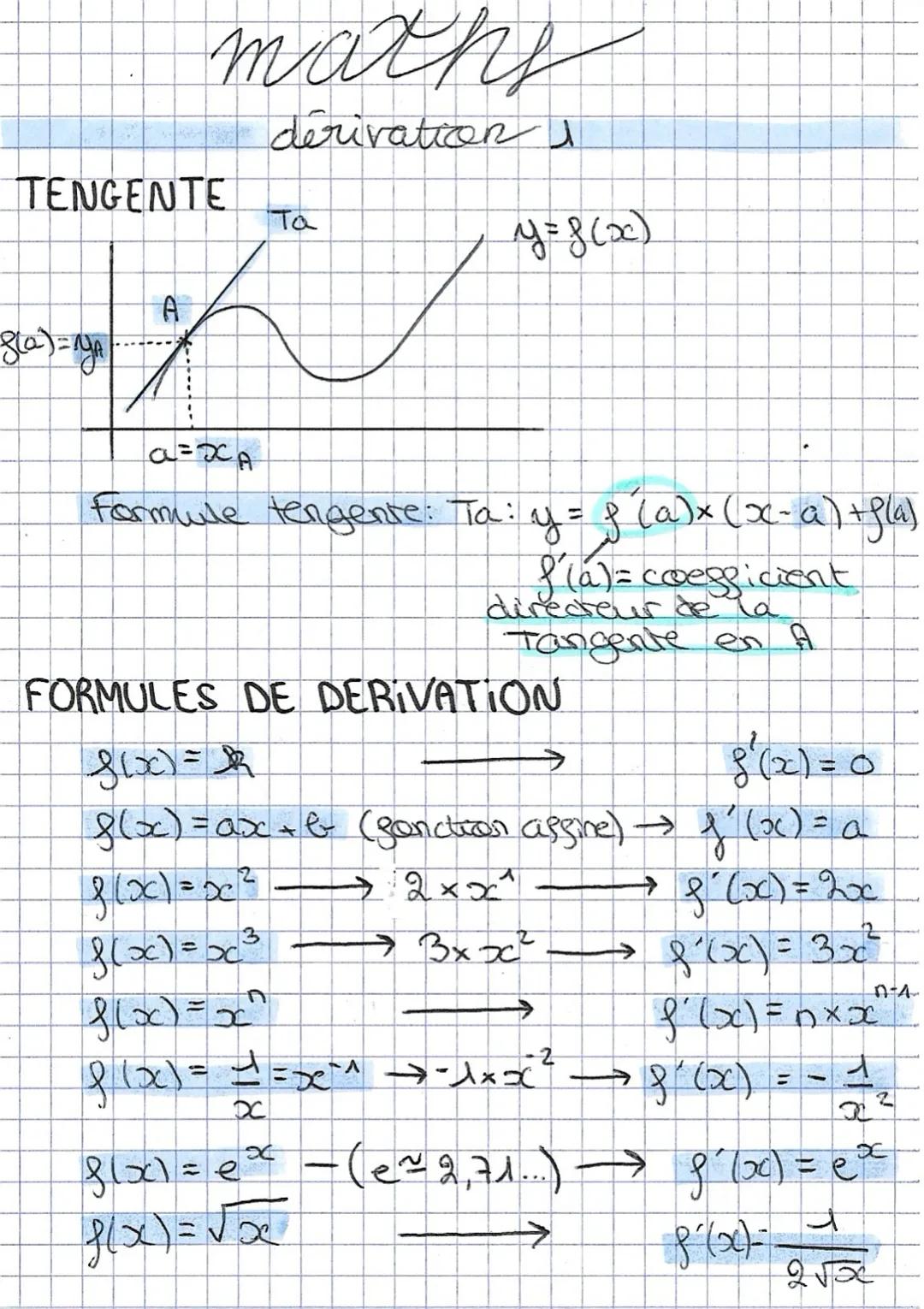
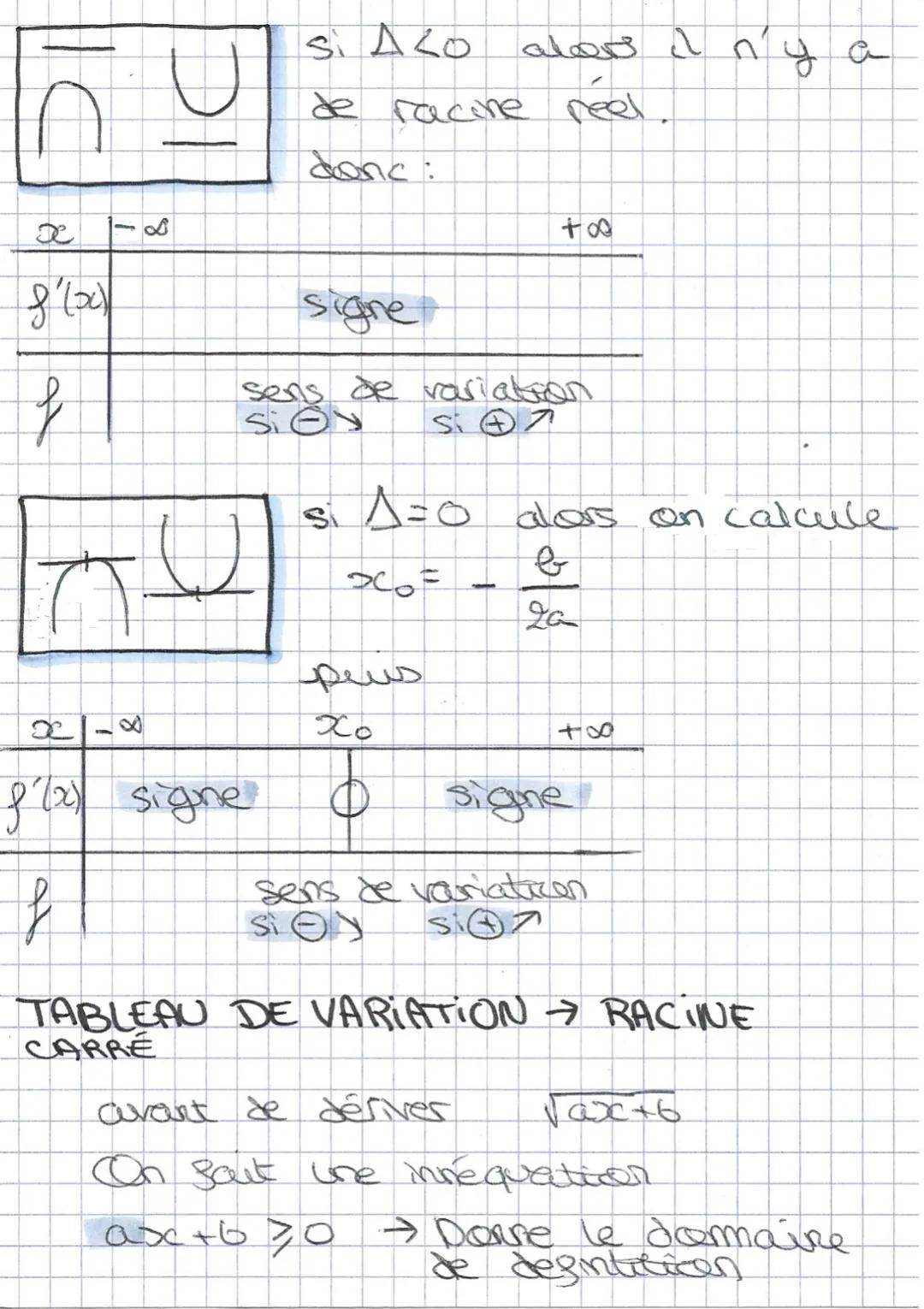
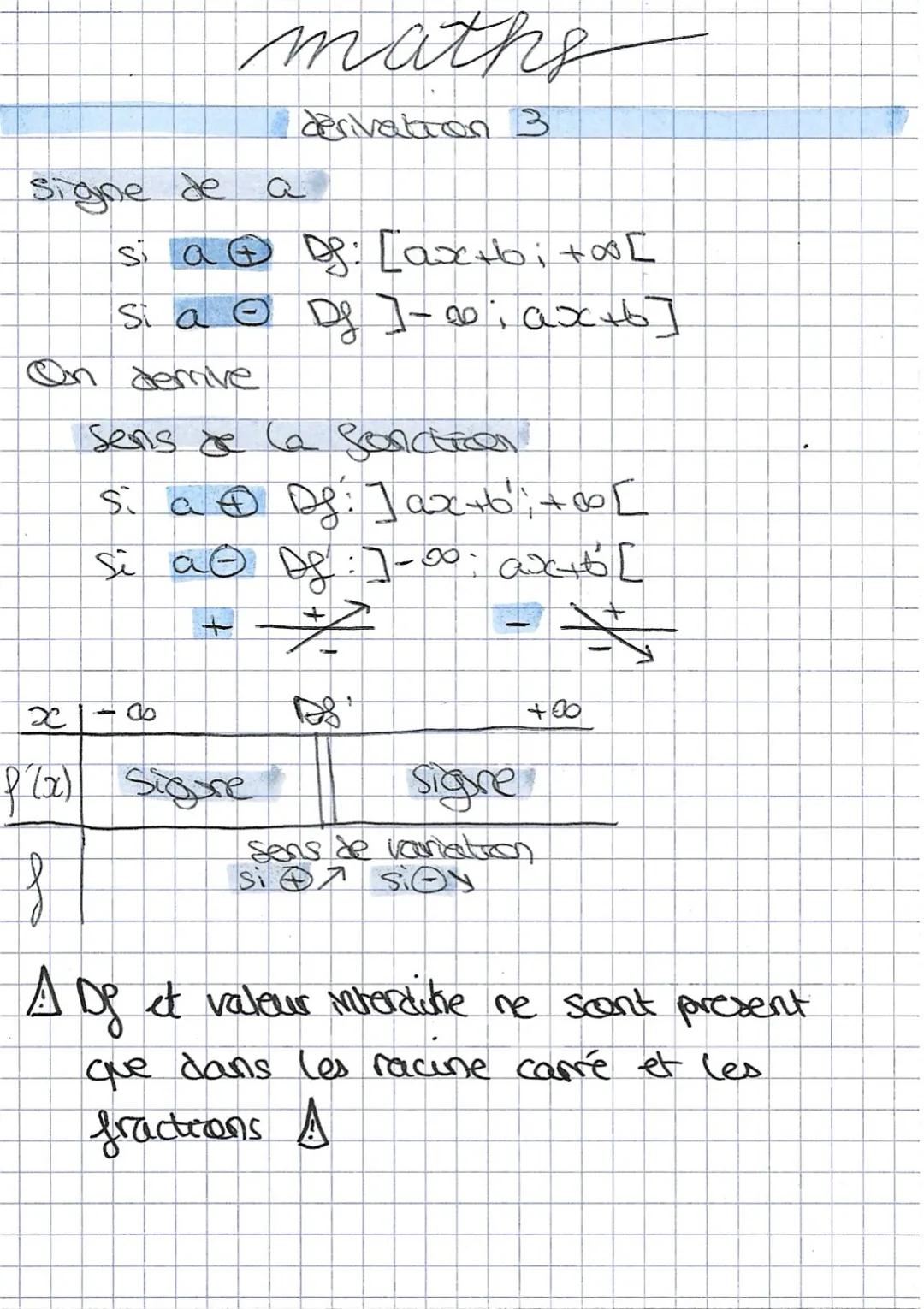
Domaines de définition et racines carrées

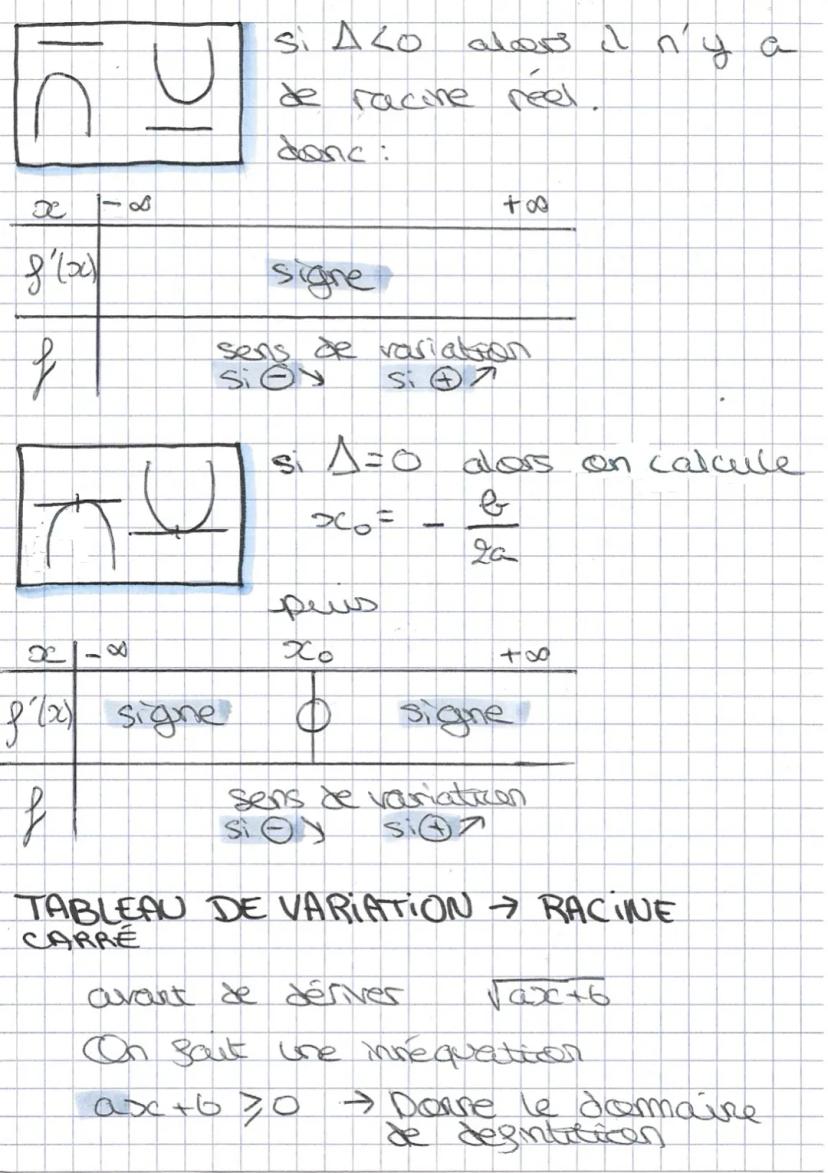
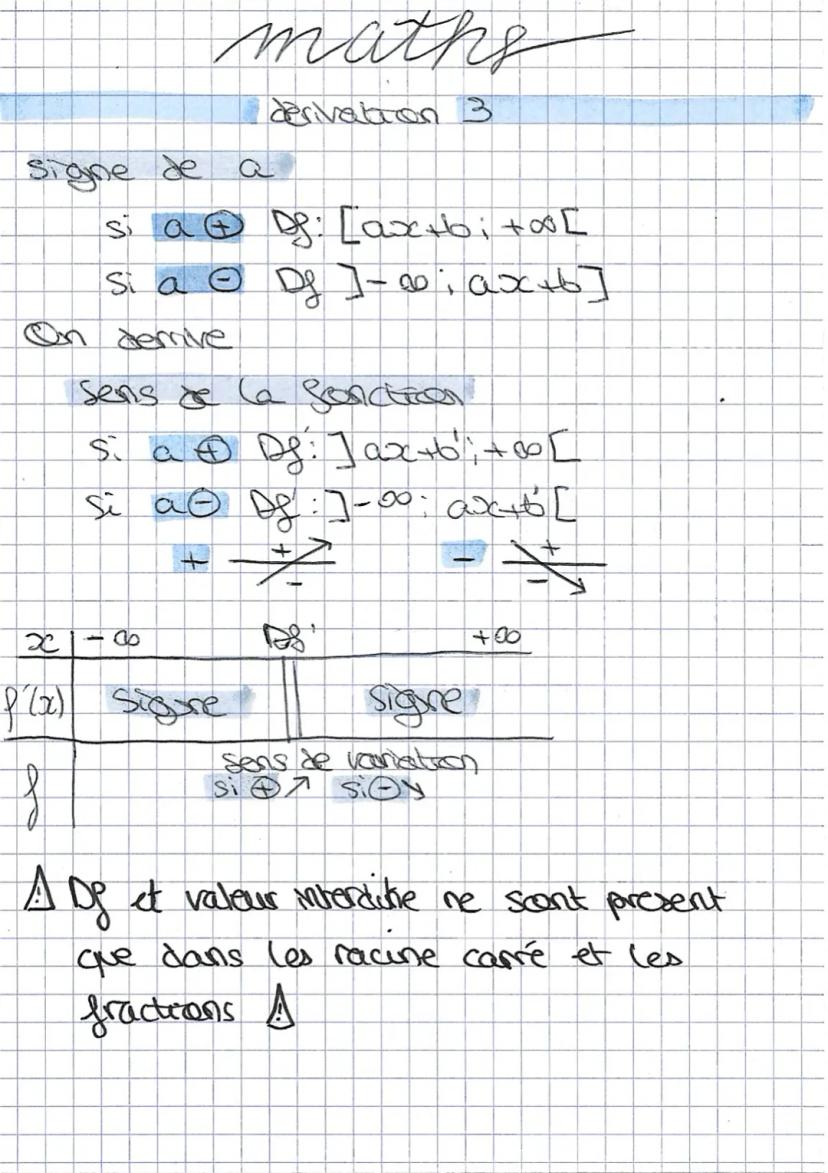
Pour les racines carrées, le domaine de définition Df dépend du signe de a. Si a > 0 : Df = [solution ; +∞[. Si a < 0 : Df = ]-∞ ; solution].

Une fois que tu as dérivé ta fonction racine carrée, le sens de variation suit une logique précise. Si a > 0, la fonction est croissante sur son domaine. Si a < 0, elle est décroissante.

Ton tableau de variation ne couvre que le domaine de définition ! Les valeurs interdites n'apparaissent que dans les racines carrées et les fractions.

La dérivée de √$ax+b$ est a/$2√(ax+b)$. Le signe dépend uniquement du signe de a, puisque le dénominateur est toujours positif sur le domaine.

Rappel : Les domaines de définition et valeurs interdites ne concernent que les racines carrées et les fractions !