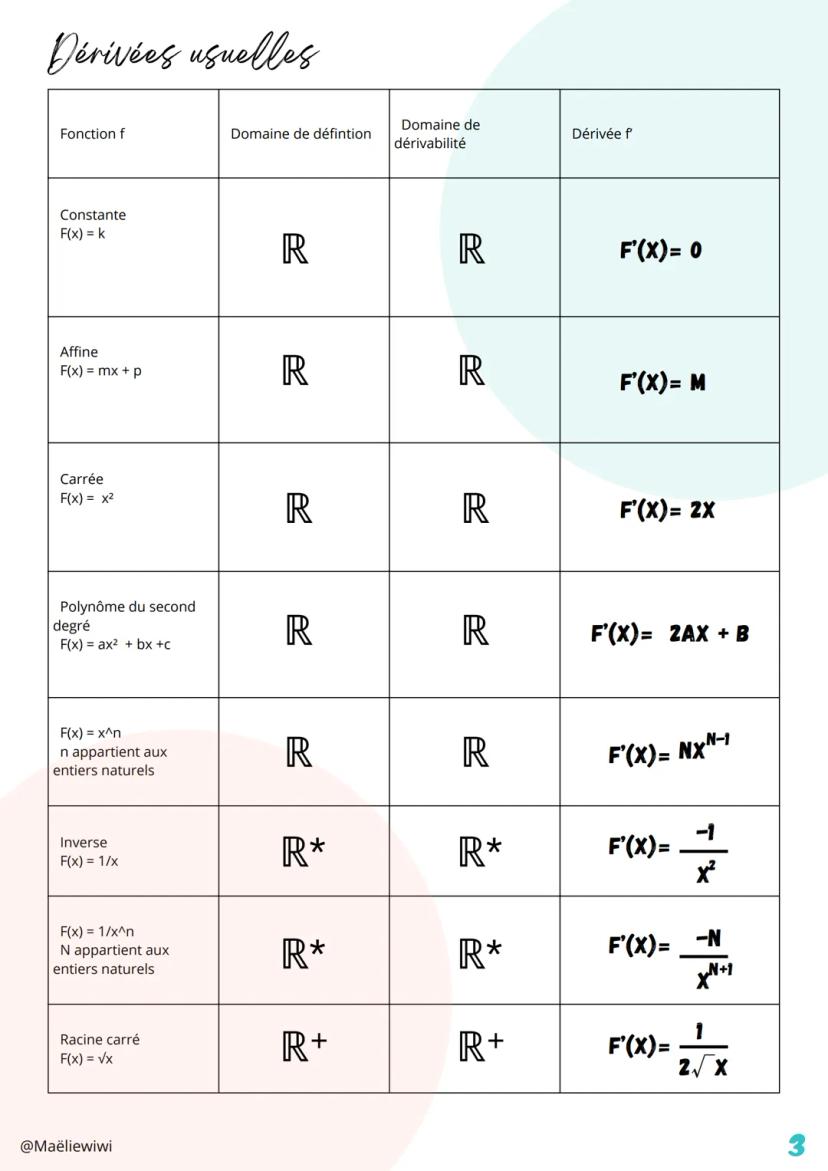
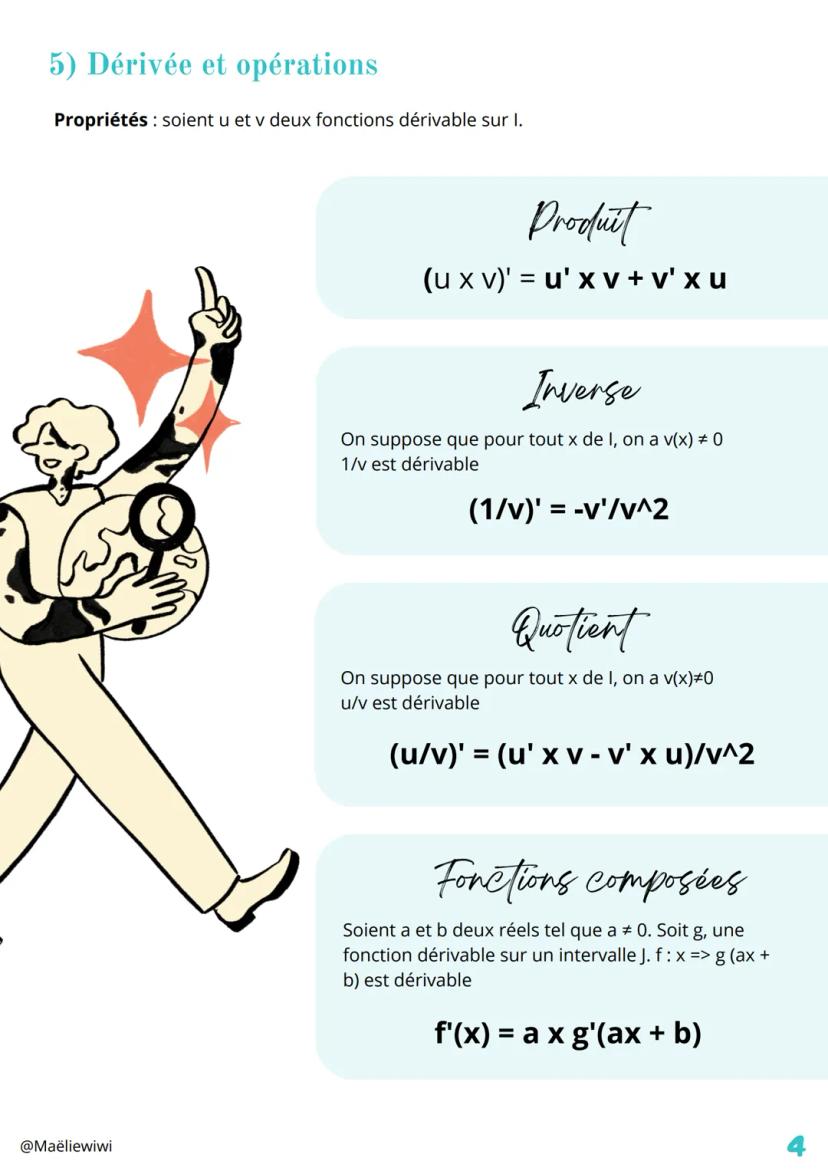
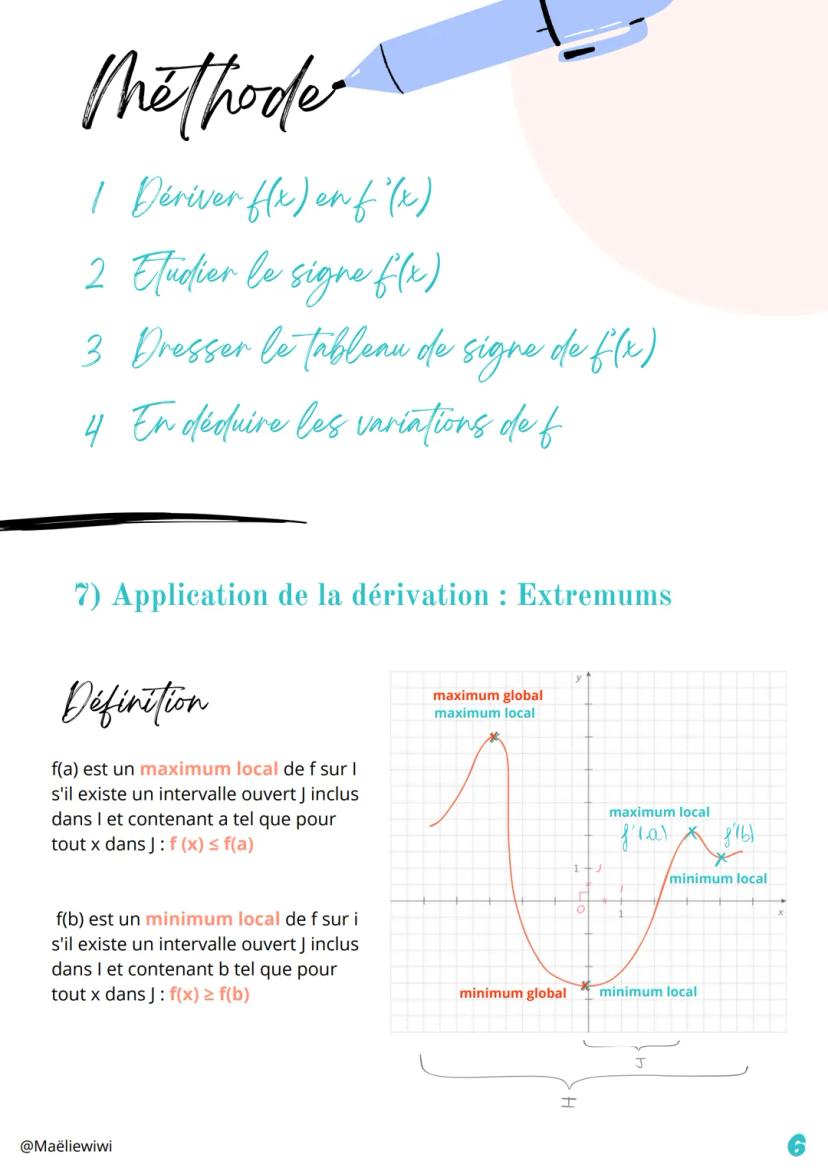
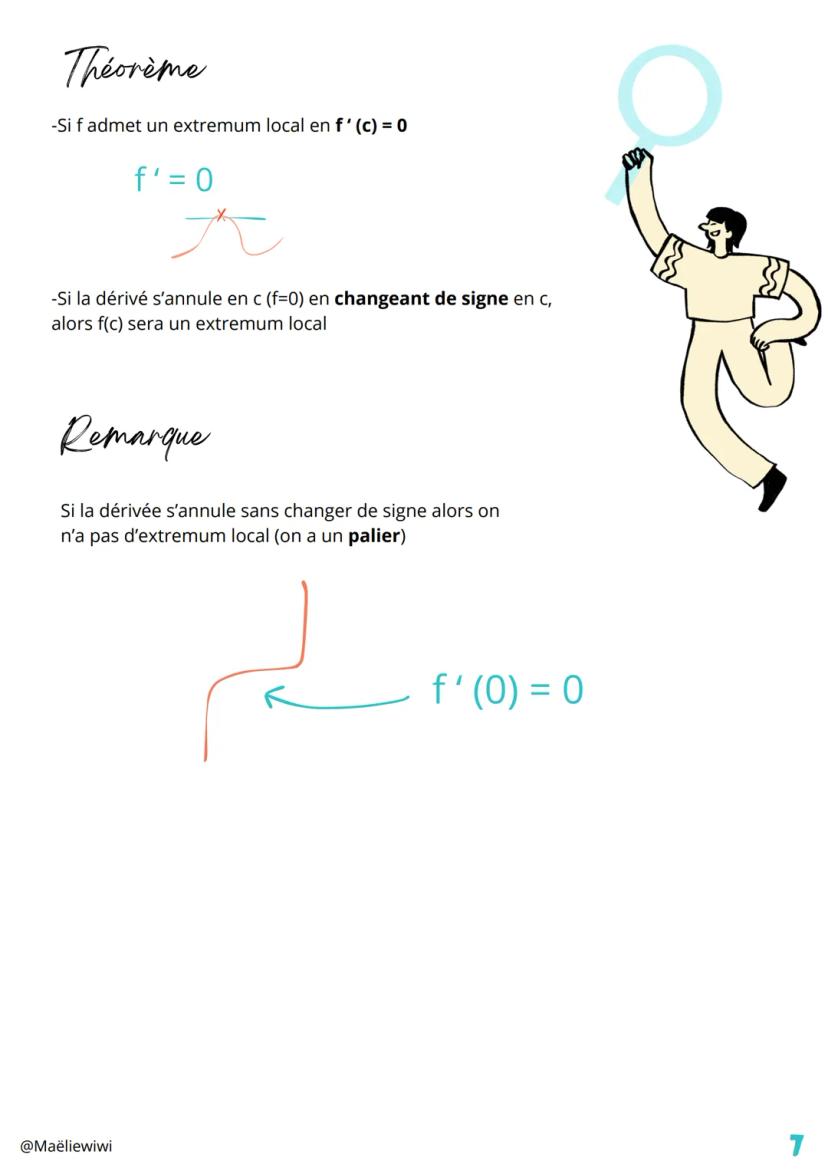
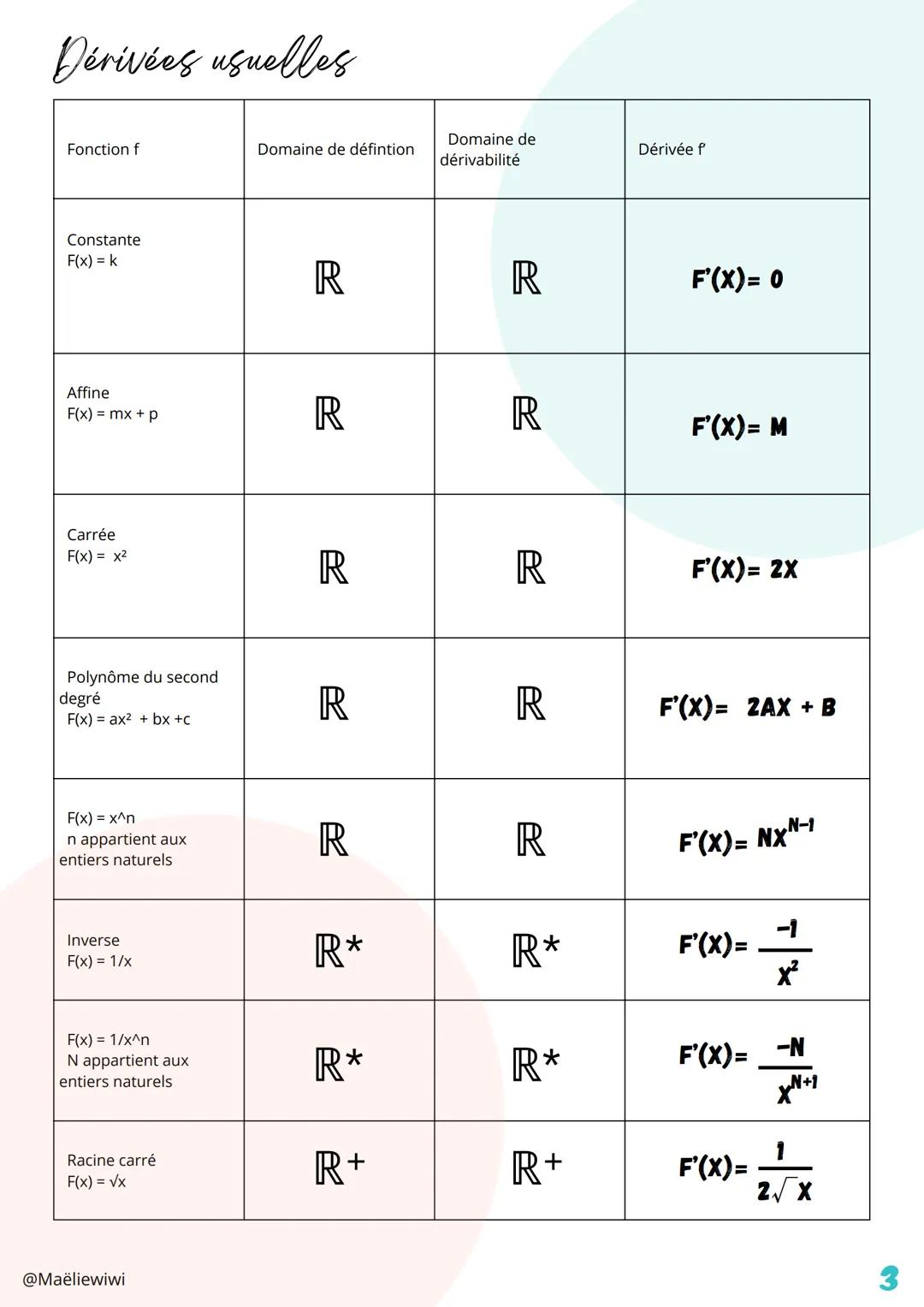
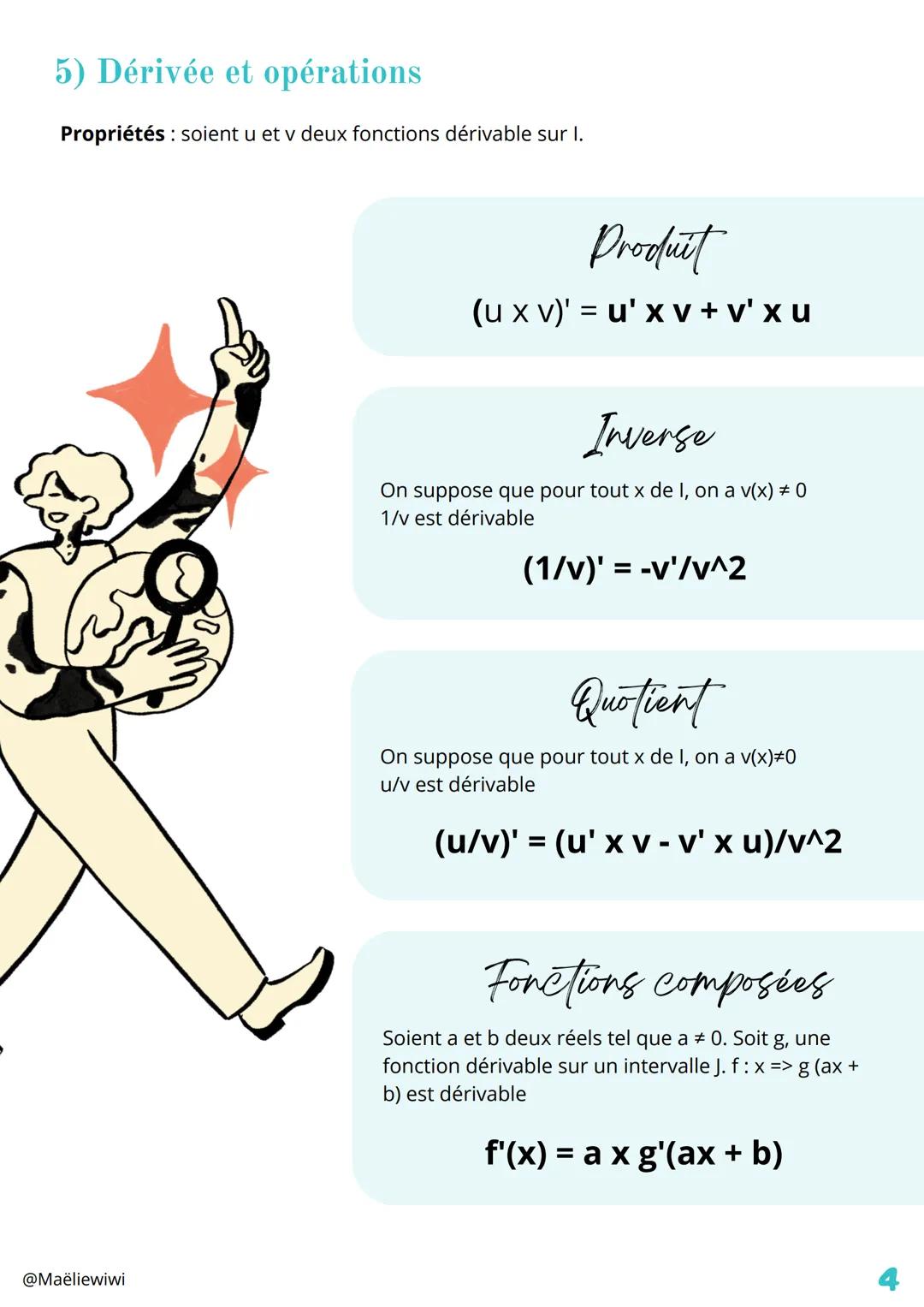
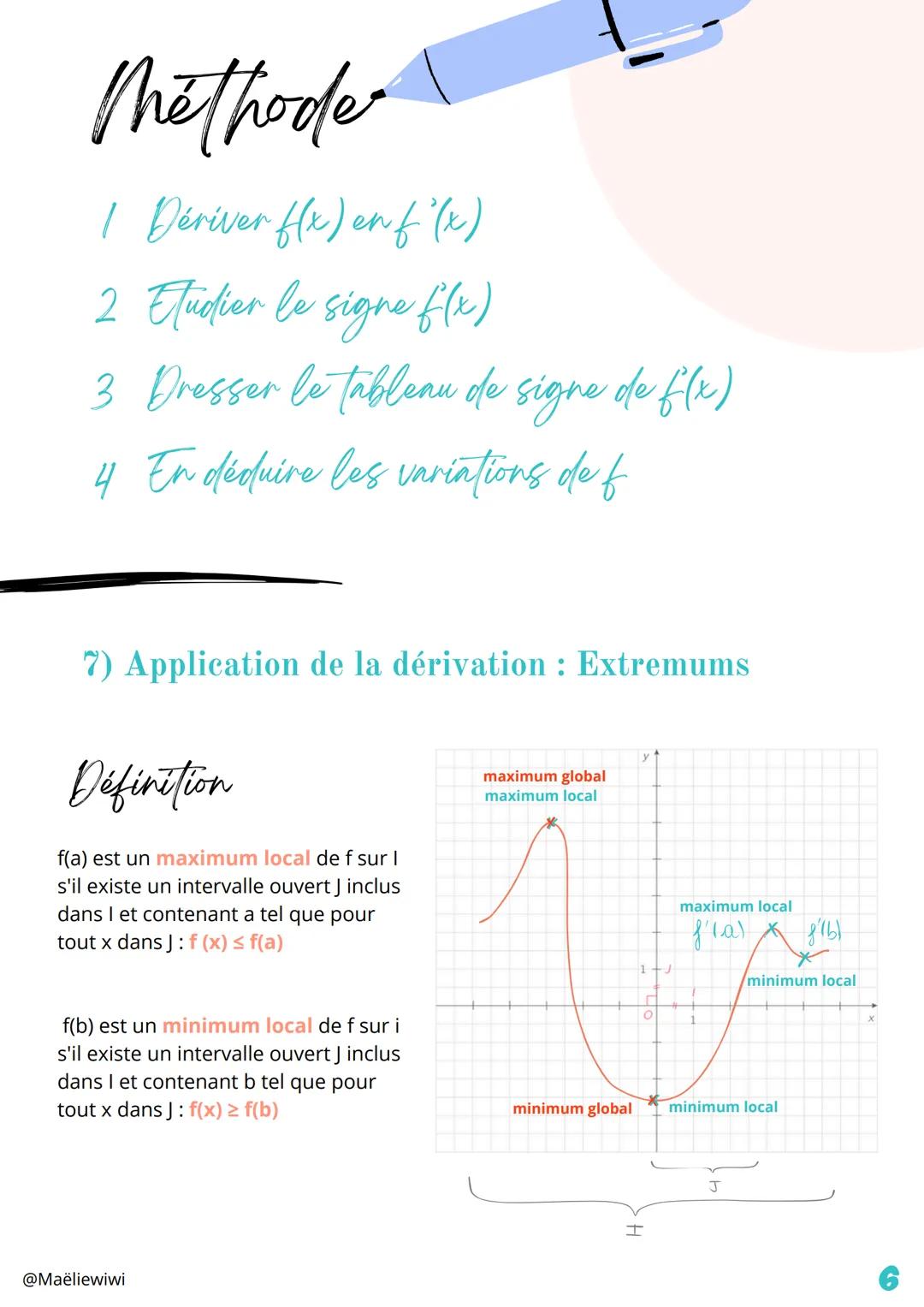
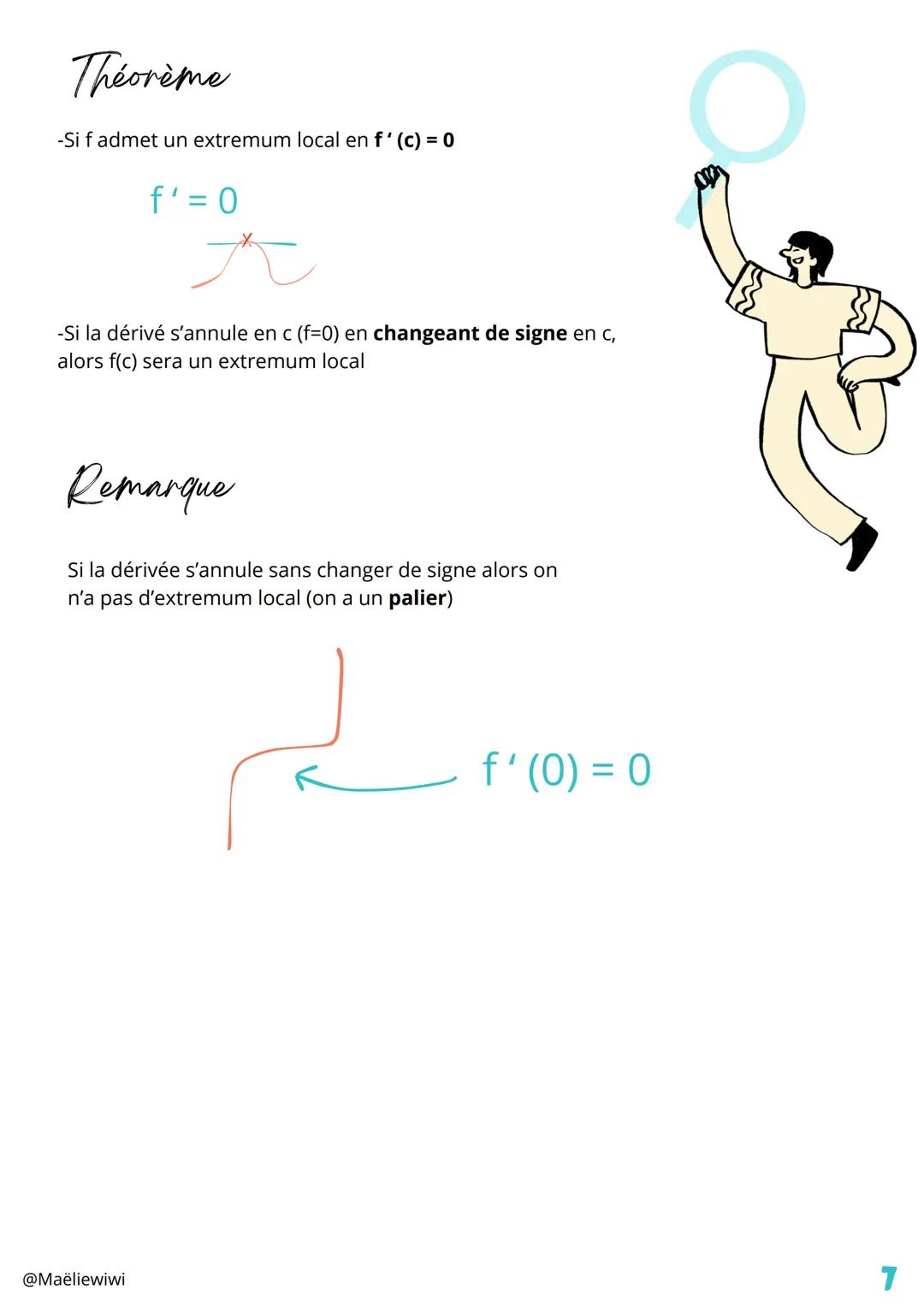
La dérivation est un outil super puissant qui permet de... Affiche plus
Inscris-toi pour voir le contenuC'est gratuit!
Accès à tous les documents
Améliore tes notes
Rejoins des millions d'étudiants
En t'inscrivant, tu acceptes les Conditions d'utilisation et la Politique de confidentialité.