Analyse du nombre de solutions avec le discriminant
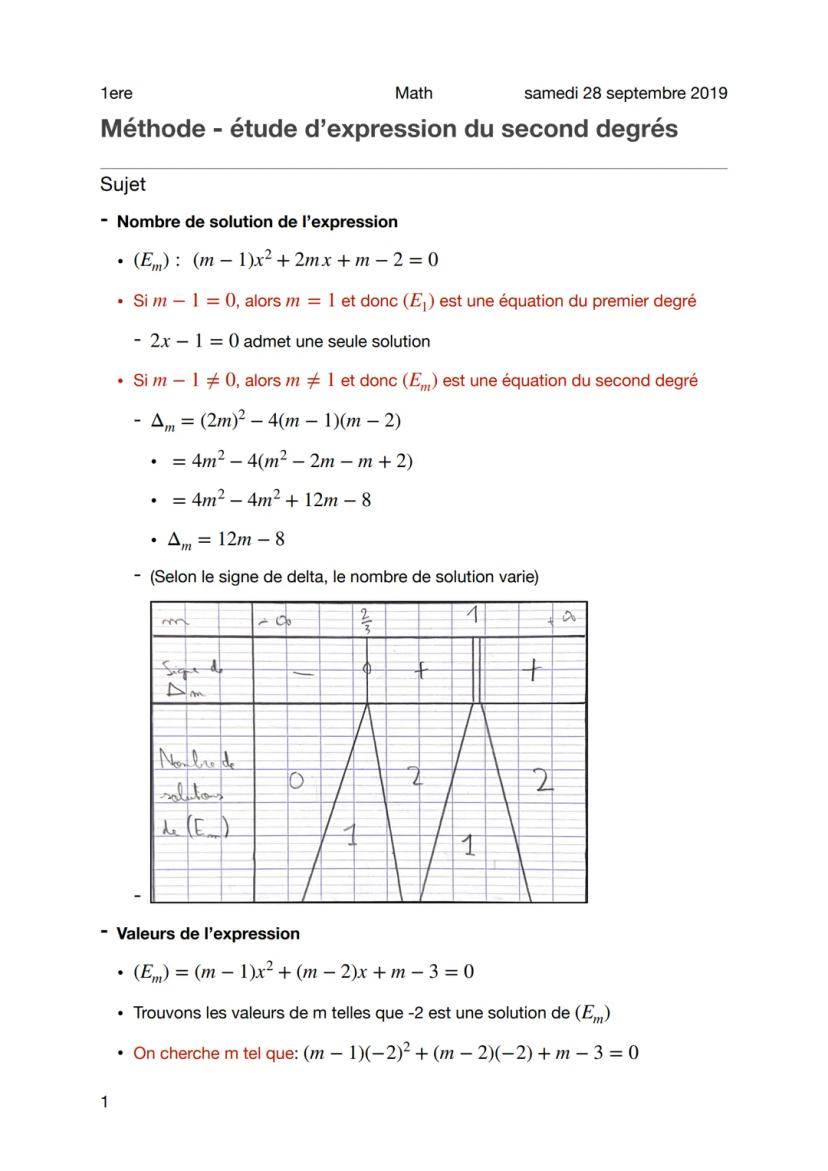
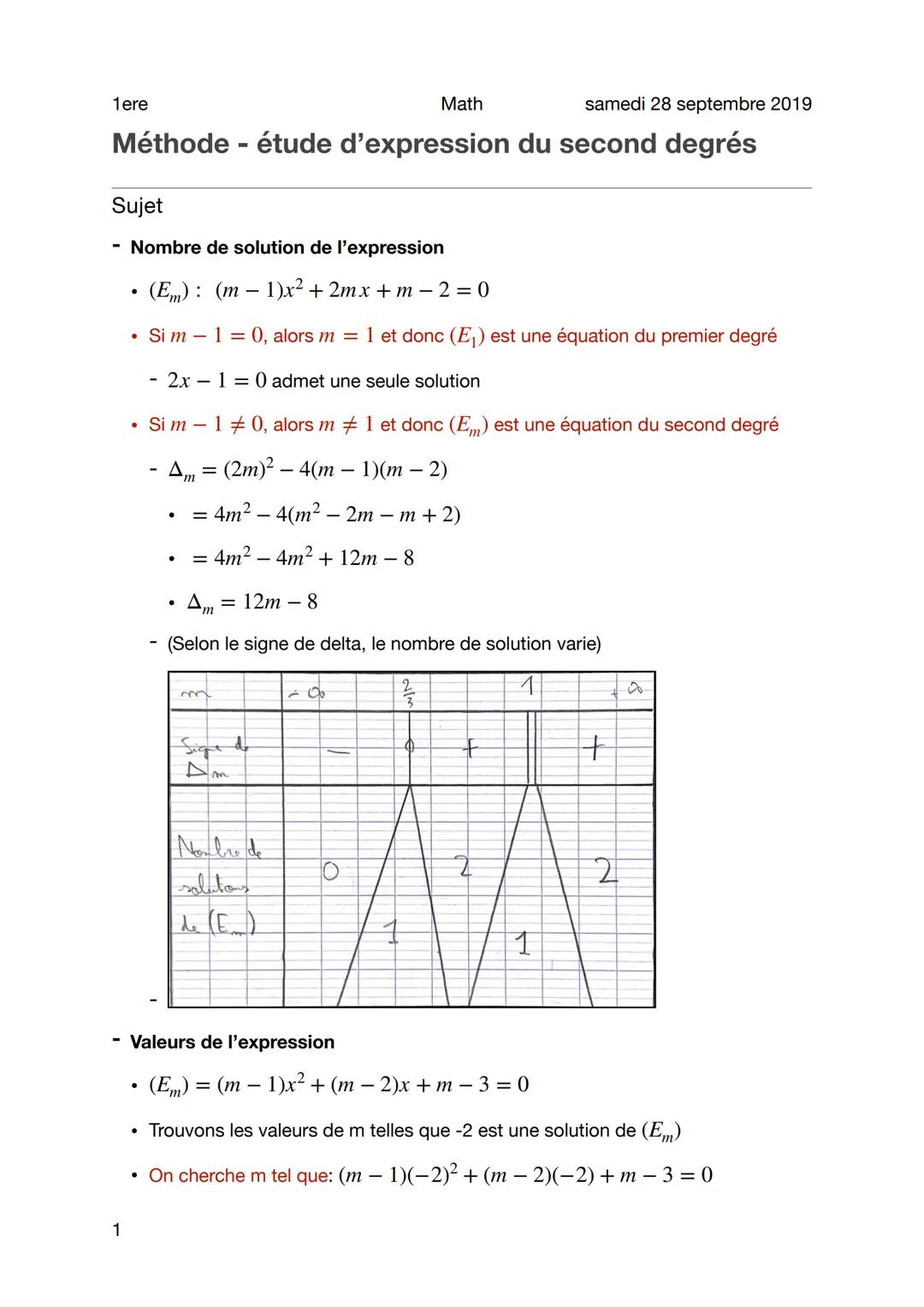
Reprenons avec l'équation (Em): m−1x² + m−2x - 3 = -m. Après remaniement, on obtient m−1x² + m−2x + m−3 = 0. Encore une fois, si m = 1, c'est du premier degré avec une solution unique.
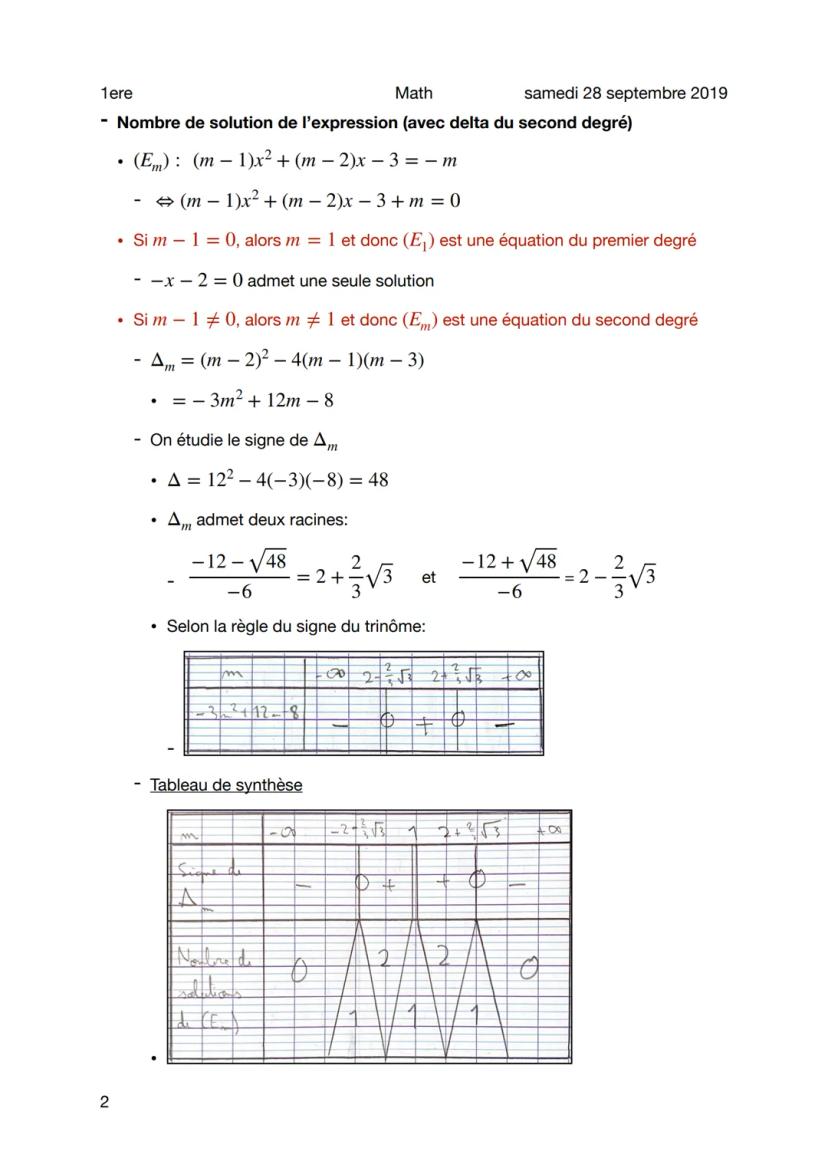
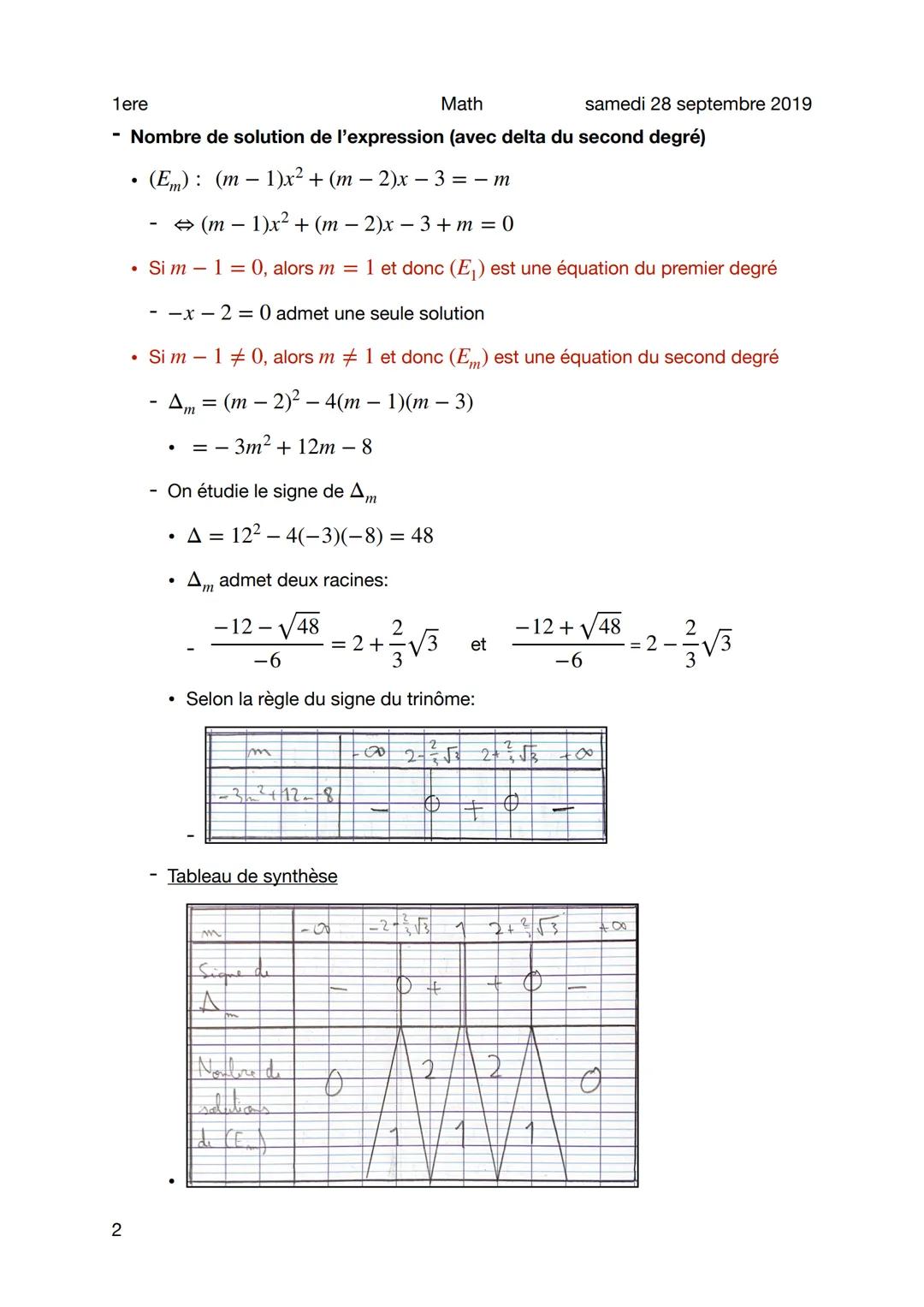
Pour m ≠ 1, le discriminant devient Δm = m−2² - 4m−1m−3 = -3m² + 12m - 8. Pour étudier son signe, tu cherches ses racines en résolvant -3m² + 12m - 8 = 0.
Les racines sont m₁ = 2 - (2√3)/3 et m₂ = 2 + (2√3)/3. Grâce à la règle du signe du trinôme, tu sais que Δm > 0 entre les racines (deux solutions), Δm = 0 aux racines (une solution), et Δm < 0 ailleurs (pas de solution).
💡 À retenir : Le signe du discriminant détermine tout : positif = 2 solutions, nul = 1 solution, négatif = 0 solution !