Exponentielle et Logarithme Népérien

Tu vas découvrir deux fonctions qui sont partout dans les sciences : l'exponentielle et le logarithme népérien. Ces fonctions sont inverses l'une de l'autre et apparaissent constamment dans les exercices du bac.

Pour l'exponentielle, tu dois savoir faire sa représentation graphique (elle passe par (0,1) et croît très vite), calculer sa dérivée $qui est égale à elle-même !$, et résoudre des équations comme e^x = 5. Les croissances comparées te montrent que l'exponentielle "gagne" toujours contre les polynômes quand x tend vers l'infini.

Le logarithme népérien ln(x) n'existe que pour x > 0. Sa courbe passe par (1,0) et croît lentement. Tu dois maîtriser son domaine de définition, résoudre des équations avec ln, et utiliser ses propriétés : ln(ab) = ln(a) + ln(b).

Astuce : Pour résoudre e^x = k, tu écris x = ln(k). Pour résoudre ln(x) = k, tu écris x = e^k.

Limites et Convexité

Les limites de fonctions te permettent de comprendre le comportement d'une fonction aux "extrémités". Quand tu rencontres des formes indéterminées comme ∞/∞, tu peux utiliser plusieurs techniques pour les lever.

Tu as trois outils puissants : la factorisation (sortir le terme dominant), les identités remarquables, et la quantité conjuguée pour les racines. Les théorèmes des gendarmes et de comparaison t'aident quand une fonction est "coincée" entre deux autres.

La convexité décrit la "courbure" d'une fonction. Une fonction convexe a une courbe qui "sourit" (comme x²), une fonction concave "fait la tête" $comme -x²$. Le lien avec la dérivée seconde est simple : f''(x) > 0 ⟹ f convexe.

Point clé : Un point d'inflexion est là où la courbe change de courbure, donc où f''(x) = 0 et f'' change de signe.

Dérivation et Continuité

La dérivation mesure la "vitesse de changement" d'une fonction. Le taux d'accroissement $f(a+h) - f(a)$/h devient la dérivée f'(a) quand h tend vers 0.

Tu dois connaître les dérivées usuelles par cœur et savoir dériver les fonctions composées avec la règle (f∘g)'(x) = f'(g(x)) × g'(x). L'équation de la tangente en a est y = f'(a)$x-a$ + f(a).

La continuité signifie qu'on peut dessiner la courbe "sans lever le crayon". Une fonction est continue en a si lim f(x) = f(a) quand x→a. Si une fonction est dérivable, elle est automatiquement continue.

Le Théorème des Valeurs Intermédiaires (TVI) est super utile : si f est continue sur [a,b] et si k est entre f(a) et f(b), alors il existe c dans [a,b] tel que f(c) = k.

Méthode pratique : Pour montrer qu'une équation a une unique solution, utilise le TVI + la monotonie de la fonction.

Calcul Intégral et Fonctions Trigonométriques

Le calcul intégral calcule des aires sous les courbes. L'intégrale ∫[a→b] f(x)dx représente l'aire entre la courbe de f, l'axe des x, et les droites x=a et x=b.

Pour calculer une intégrale, tu cherches une primitive F de f, puis tu appliques F(b) - F(a). L'intégration par parties ∫u'v = [uv] - ∫uv' est parfaite quand tu as un produit. La valeur moyenne d'une fonction sur [a,b] est $1/(b-a)$ × ∫[a→b] f(x)dx.

Les fonctions trigonométriques sin(x) et cos(x) sont périodiques de période 2π. Tu dois savoir que (sin(x))' = cos(x) et (cos(x))' = -sin(x). Ces fonctions sont respectivement impaire et paire.

Pour résoudre sin(x) = k, tu cherches x = arcsin(k) + 2πn ou x = π - arcsin(k) + 2πn. Les variations : sin croît sur [-π/2, π/2], cos décroît sur [0, π].

Rappel essentiel : Les primitives de sin et cos sont -cos et sin respectivement, à une constante près.

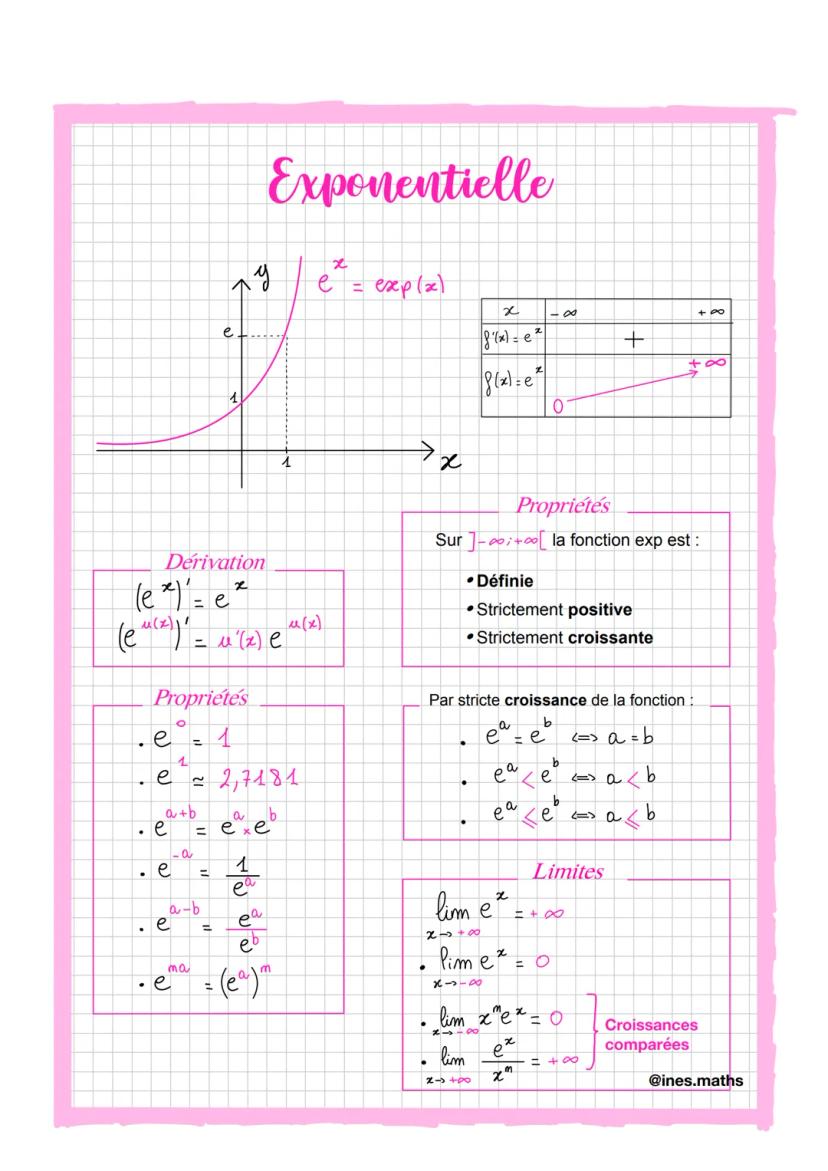
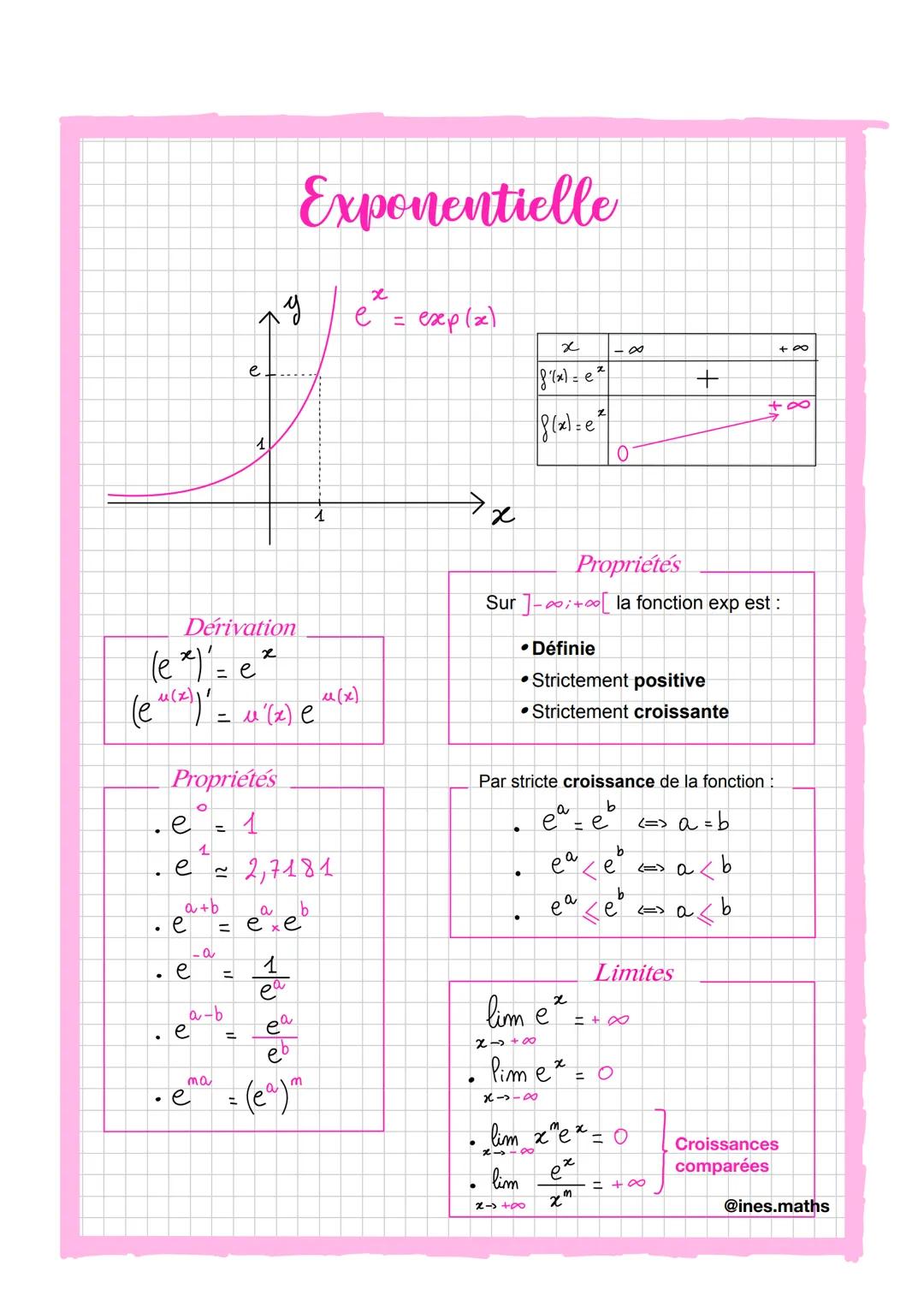
Les Suites

Les suites sont des listes ordonnées de nombres. Pour étudier leur sens de variation, tu peux calculer u_{n+1} - u_n (si >0, croissante) ou u_{n+1}/u_n $si >1 et u_n>0, croissante$.

Une suite est convergente si ses termes se rapprochent d'une valeur finie. Les suites arithmétiques $de la forme u_n = u_0 + nr$ divergent sauf si r = 0. Les suites géométriques $u_n = u_0 × q^n$ convergent vers 0 si |q| < 1.

Le théorème des gendarmes est génial : si u_n ≤ v_n ≤ w_n et si u_n et w_n tendent vers la même limite L, alors v_n tend aussi vers L. Le théorème de comparaison compare les comportements à l'infini.

Pour les formes indéterminées comme ∞ - ∞, tu peux factoriser par le terme dominant ou utiliser la quantité conjuguée. Le théorème du point fixe te dit que si une suite définie par u_{n+1} = f$u_n$ converge vers l, alors f(l) = l.

Méthode récurrence : Pour démontrer une propriété par récurrence, vérifie l'initialisation, puis montre que si c'est vrai au rang n, c'est vrai au rang n+1.

Probabilités et Géométrie dans l'Espace

En probabilités, les probabilités conditionnelles P(A|B) mesurent la chance que A se réalise sachant que B s'est réalisé. La formule P(A|B) = P(A∩B)/P(B) est fondamentale.

Les arbres de probabilités visualisent parfaitement les situations. La formule des probabilités totales dit que P(A) = P(A|B)×P(B) + P(A|B̄)×P(B̄). La loi binomiale compte le nombre de succès dans n expériences identiques.

En géométrie dans l'espace, tu travailles avec des vecteurs en 3D. Trois points sont alignés si leurs vecteurs sont colinéaires. Trois points sont coplanaires s'ils appartiennent au même plan.

Les vecteurs colinéaires ont même direction (l'un est multiple de l'autre). Pour trouver l'intersection de deux plans ou droites, tu résous des systèmes d'équations paramétriques.

Astuce géométrie : Visualise toujours en 3D ! Dessine des schémas même approximatifs pour mieux comprendre les situations.

Produit Scalaire et Orthogonalité

Le produit scalaire dans l'espace se calcule de trois façons : avec les coordonnées $⃗u·⃗v = x₁x₂ + y₁y₂ + z₁z₂$, avec le cosinus $⃗u·⃗v = ||⃗u|| × ||⃗v|| × cos θ$, ou avec la projection orthogonale.

Deux vecteurs sont orthogonaux quand leur produit scalaire est nul. Un vecteur normal à un plan est orthogonal à tous les vecteurs du plan. Deux plans sont orthogonaux si leurs vecteurs normaux sont orthogonaux.

En orthogonalité et distances, distingue bien : deux droites sont orthogonales si leurs vecteurs directeurs le sont, elles sont perpendiculaires si elles sont orthogonales ET sécantes. Une droite est orthogonale à un plan si elle est orthogonale à tout vecteur du plan.

La distance d'un point A à un plan se calcule avec la formule utilisant l'équation cartésienne du plan. Le projeté orthogonal d'un point sur une droite ou un plan est le point le plus proche.

Méthode pratique : Pour montrer qu'une droite est orthogonale à un plan, montre qu'elle est orthogonale à deux vecteurs non colinéaires du plan.

Représentations Paramétriques et Équations Cartésiennes

Les représentations paramétriques décrivent les objets géométriques avec des paramètres. Pour une droite passant par A avec vecteur directeur ⃗u, tu écris M = A + t⃗u, soit x = x_A + tu₁, y = y_A + tu₂, z = z_A + tu₃.

Un plan défini par un point A et deux vecteurs ⃗u et ⃗v s'écrit M = A + s⃗u + t⃗v. Pour vérifier qu'un point appartient à un plan, tu substitues ses coordonnées dans l'équation paramétrique.

L'équation cartésienne d'un plan est de la forme ax + by + cz + d = 0, où (a,b,c) est un vecteur normal. Pour une droite dans l'espace, l'équation cartésienne est l'intersection de deux plans.

Passer du paramétrique au cartésien : élimine les paramètres des équations paramétriques. Passer du cartésien au paramétrique : trouve un point particulier et des vecteurs directeurs (ou normaux).

Conseil : Les représentations paramétriques sont souvent plus pratiques pour les calculs, les équations cartésiennes pour les propriétés générales.

Propriétés de l'Exponentielle

La fonction exponentielle e^x = exp(x) est définie sur ℝ tout entier et strictement positive. Sa courbe passe par (0,1) et croît de façon spectaculaire : elle vaut environ 2,718 en x=1.

Sa dérivée est remarquable : $e^x$' = e^x ! Pour une composée e^u(x), tu obtiens $e^u(x)$' = u'(x) × e^u(x). C'est la seule fonction égale à sa propre dérivée (à un facteur près).

Les propriétés algébriques sont cruciales : e^$a+b$ = e^a × e^b, e^$a-b$ = e^a/e^b, $e^a$^m = e^(am). Par stricte croissance : e^a = e^b ⟺ a = b, et e^a < e^b ⟺ a < b.

Les limites et croissances comparées montrent que l'exponentielle "bat" tous les polynômes : lim$x→+∞$ e^x/x^n = +∞ pour tout n. En -∞, elle tend vers 0, et lim$x→-∞$ xe^x = 0.

Formule clé : e^0 = 1, e^1 ≈ 2,718, et e^$-x$ = 1/e^x. Ces relations sont constamment utilisées !

Méthodes pour l'Exponentielle

Pour résoudre une équation avec exp(x), commence par rassembler les termes exponentiels d'un côté. Utilise ensuite les propriétés de base de l'exponentielle.

Type 1 : équation e^(quelque chose) = nombre. Si e^(2x) = 7, alors 2x = ln(7), donc x = ln(7)/2. Tu utilises le fait que exp et ln sont réciproques.

Type 2 : équation entre deux exponentielles. Si e^(2x²) = e^8, alors les exposants sont égaux : 2x² = 8, donc x² = 4, et x = ±2. La stricte croissance de exp te permet cette simplification.

Type 3 : inéquation avec exponentielle. Pour e^(4x) < 3, tu appliques ln (croissant) aux deux membres : 4x < ln(3), donc x < ln(3)/4. Attention au sens de l'inégalité !

Piège à éviter : ln(a) n'existe que si a > 0. Vérifie toujours que tu peux appliquer ln avant de le faire !