Introduction au second degré

Une fonction polynomiale de degré deux (ou trinôme du second degré) s'écrit sous la forme f(x) = ax² + bx + c, où a ≠ 0. Cette fonction est définie sur l'ensemble des réels ℝ.

Dans ce chapitre, nous allons apprendre à résoudre des équations du second degré de la forme ax² + bx + c = 0. Ces équations ne sont pas nouvelles dans l'histoire des mathématiques ! Les Babyloniens les étudiaient déjà au 8ème siècle avant J.-C., et Al-Khwarizmi (dont le nom a donné le mot "algorithme") a développé des méthodes de résolution au 9ème siècle.

Les polynômes du second degré sont très utiles dans la vie réelle. Ils permettent de décrire la trajectoire d'un cycliste après un tremplin, de modéliser l'évolution des naissances lors d'un baby-boom, ou encore de résoudre des problèmes d'optimisation de formes géométriques.

💡 Une particularité fascinante des équations du second degré est qu'elles peuvent avoir 0, 1 ou 2 solutions - contrairement aux équations du premier degré qui en ont toujours exactement une.

Rappels et forme canonique

Pour bien maîtriser ce chapitre, assurez-vous de connaître vos identités remarquables et de savoir résoudre des équations simples comme ax + b = 0 ou x² - 9 = 0.

Tout polynôme du second degré f(x) = ax² + bx + c peut s'écrire sous une forme très pratique appelée forme canonique :

f(x) = a$(x + b/2a)² - Δ/(4a²)$

où Δ = b² - 4ac est appelé le discriminant du polynôme.

Pour obtenir cette forme, on utilise une astuce qui consiste à compléter le carré. Voici comment procéder :

1. On factoriser a : f(x) = a$x² + (b/a)x + c/a$
2. On reconnaît le début d'une identité remarquable
3. On complète le carré et on réorganise les termes

Par exemple, si f(x) = x² + x + 1, on peut l'écrire sous la forme canonique f(x) = $x + 1/2$² + 3/4.

Cette forme est particulièrement utile car elle permet de :

• Identifier facilement l'extremum de la fonction
• Déterminer rapidement les racines du polynôme
• Visualiser la forme de la parabole associée

💡 La forme canonique est comme une carte d'identité du polynôme : elle révèle immédiatement ses caractéristiques essentielles !

Résolution d'équations du second degré

Pour résoudre une équation du second degré (E) : ax² + bx + c = 0, le discriminant Δ = b² - 4ac est notre meilleur allié !

En fonction de la valeur de Δ, trois cas se présentent :

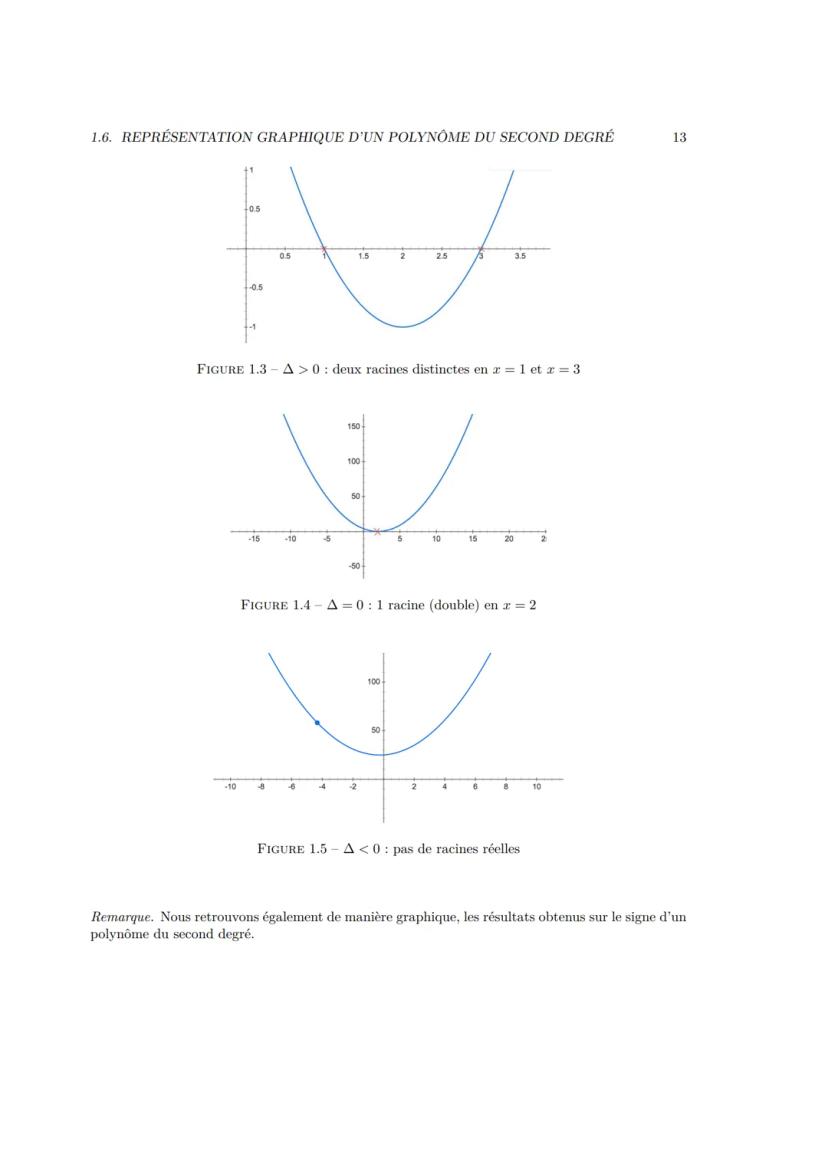
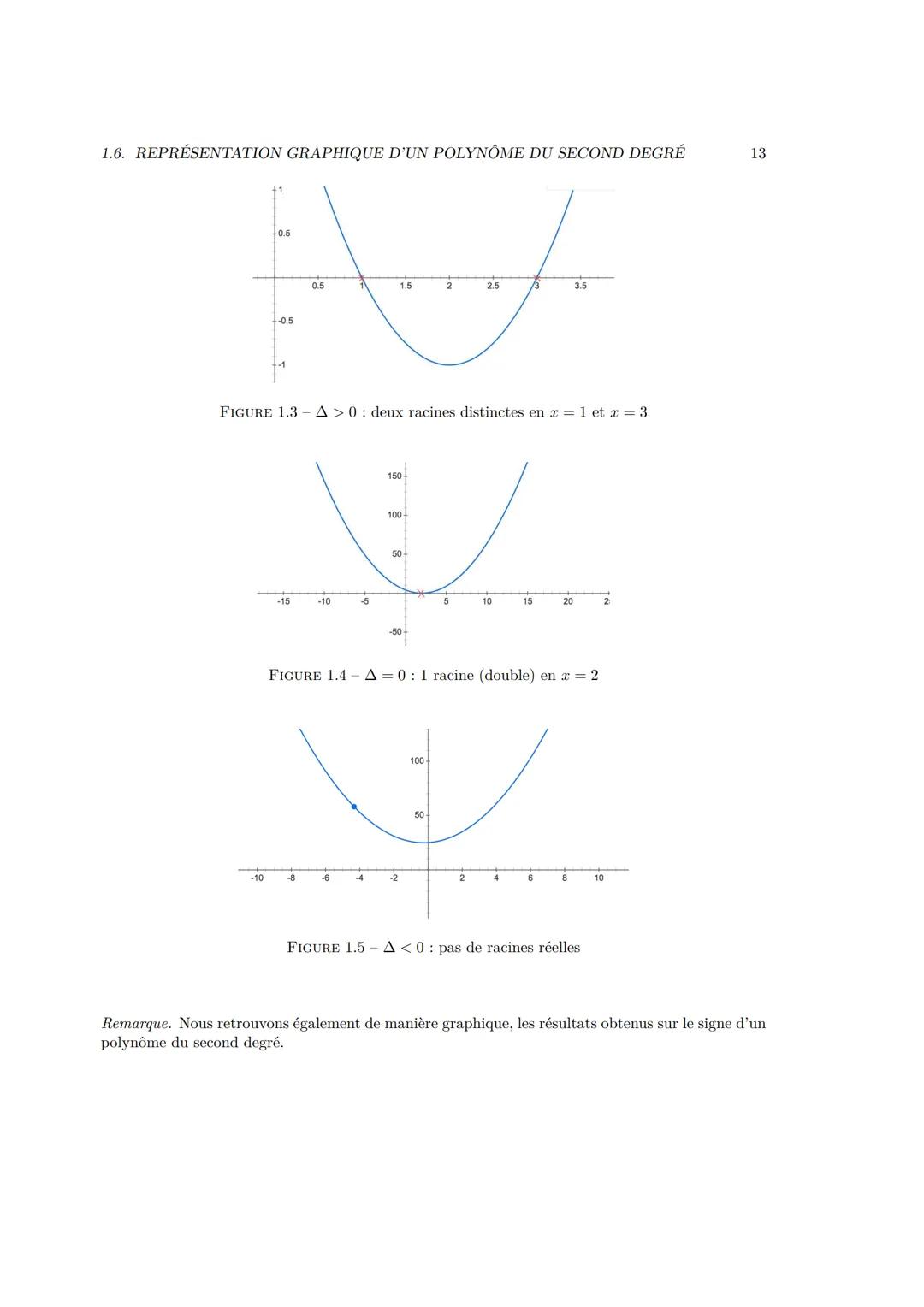
1. Si Δ > 0 : l'équation admet deux solutions réelles distinctes x₁ = $-b + √Δ$ / 2a et x₂ = $-b - √Δ$ / 2a

2. Si Δ = 0 : l'équation admet une solution réelle double x₀ = -b / 2a

3. Si Δ < 0 : l'équation n'admet aucune solution réelle (Plus tard en Terminale, vous découvrirez les nombres complexes qui permettent de trouver des solutions même dans ce cas !)

Pour démontrer ces résultats, on utilise la forme canonique de notre polynôme : f(x) = a$(x + b/2a)² - Δ/(4a²)$

Si Δ > 0, on peut transformer l'équation f(x) = 0 en une différence de carrés, qu'on factorise facilement grâce à l'identité a² - b² = $a+b$$a-b$.

Si Δ = 0, l'équation devient simplement $x + b/2a$² = 0, qui admet une unique solution.

Si Δ < 0, on arrive à une contradiction : un carré (toujours positif) devrait être égal à un nombre négatif, ce qui est impossible dans ℝ.

💡 La formule de résolution des équations du second degré est l'une des plus célèbres des mathématiques. Prenez le temps de la mémoriser, elle vous servira tout au long de votre parcours !

Signe d'un polynôme du second degré

Lorsqu'on connaît les racines d'un polynôme du second degré, on peut le factoriser et déterminer son signe :

1. Si Δ > 0 et que x₁ < x₂ sont les racines, alors f(x) = a$x-x₁$$x-x₂$

   • Pour x < x₁ : f(x) a le signe de a
   • Pour x₁ < x < x₂ : f(x) a le signe opposé de a
   • Pour x > x₂ : f(x) a le signe de a

2. Si Δ = 0 et que x₀ est la racine double, alors f(x) = a$x-x₀$²

   • Pour tout x ≠ x₀ : f(x) a le signe de a
   • Pour x = x₀ : f(x) = 0

3. Si Δ < 0, alors f(x) ne s'annule jamais et garde toujours le signe de a

Cette factorisation permet de dresser facilement un tableau de signe pour résoudre des inéquations comme f(x) > 0 ou f(x) ≤ 0.

Par exemple, pour résoudre 3x² - 4x + 5 < 0 :

1. On calcule Δ = 16 - 60 = -44 < 0
2. Comme Δ < 0 et a = 3 > 0, le trinôme est toujours positif
3. L'inéquation n'a donc aucune solution

💡 Pour retenir les variations de signe, pensez à une "vague" qui change de signe à chaque racine. Si a > 0, la vague part du positif, si a < 0, elle part du négatif.

Représentation graphique

La courbe représentative d'un polynôme du second degré est toujours une parabole. Sa forme canonique f(x) = a$(x-α)² + β$ nous donne directement :

• L'axe de symétrie de la parabole : la droite d'équation x = α
• Le sommet de la parabole : le point S(α, β)
• L'orientation de la parabole : vers le haut si a > 0, vers le bas si a < 0

Pour a > 0, la fonction atteint son minimum au point α, avec les variations suivantes :

• Pour x < α : f est décroissante
• Pour x > α : f est croissante

Pour a < 0, la fonction atteint son maximum au point α, avec les variations opposées.

Les racines du polynôme correspondent aux points d'intersection de la parabole avec l'axe des abscisses :

• Si Δ > 0 : la parabole coupe l'axe des abscisses en deux points
• Si Δ = 0 : la parabole est tangente à l'axe des abscisses (un seul point d'intersection)
• Si Δ < 0 : la parabole ne coupe jamais l'axe des abscisses

Cette interprétation graphique vous permet de visualiser les solutions des équations et inéquations du second degré.

💡 Pour tracer rapidement une parabole, déterminez d'abord son sommet et son axe de symétrie, puis placez les racines (si elles existent). La courbe passe par ces points et est symétrique par rapport à son axe.

Bilan et applications

Voici les compétences essentielles à maîtriser sur le second degré :

1. Résoudre une équation du second degré en calculant le discriminant Δ et en appliquant les formules appropriées
2. Manipuler les différentes formes d'un polynôme (développée, canonique, factorisée)
3. Déterminer le signe d'un polynôme du second degré et résoudre des inéquations
4. Étudier les variations et trouver l'extremum (minimum ou maximum)
5. Représenter graphiquement la parabole associée

Ces outils vous permettent de résoudre des problèmes concrets comme :

• Optimiser des distances, des aires ou des volumes
• Étudier des trajectoires
• Analyser la position relative de deux courbes
• Résoudre des équations de degré supérieur par changement de variable

Le second degré est un outil mathématique puissant qui vous servira dans de nombreux contextes, des sciences physiques à l'économie.

💡 Pour résoudre efficacement des problèmes d'optimisation, cherchez toujours à exprimer la grandeur à optimiser sous forme d'un polynôme du second degré, puis utilisez la forme canonique pour trouver son extremum.