Calcul pratique et variations
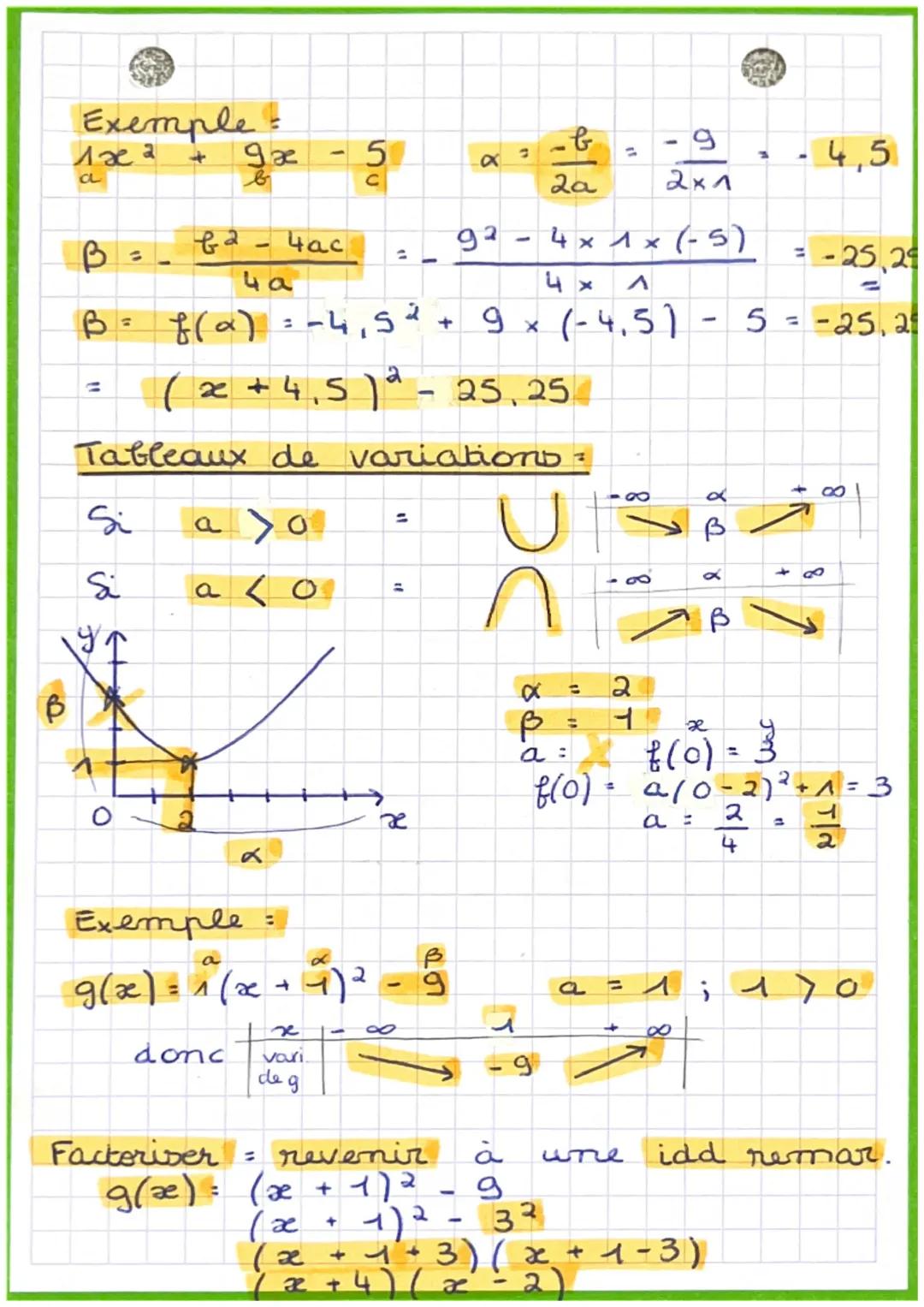
Prenons un exemple concret : f(x) = x² + 9x - 5. Pour trouver la forme canonique, tu calcules d'abord α = -9/(2×1) = -4,5, puis β = f(-4,5) = -25,25. Donc f(x) = x+4,5² - 25,25.
Le tableau de variations dépend du signe de a : si a > 0, ta parabole a la forme d'un U (elle "sourit"), si a < 0, elle a la forme d'un ∩ (elle "boude"). Le sommet se trouve toujours en x = α.
Pour factoriser, tu peux utiliser l'identité remarquable a² - b². Par exemple, avec g(x) = x+1² - 9, tu reconnais x+1² - 3², ce qui donne x+1+3x+1−3 = x+4x−2.
💡 Méthode : Repère les formes a² - b² pour factoriser rapidement avec les identités remarquables !