Le théorème des valeurs intermédiaires
Tu te demandes quand utiliser le TVI ? C'est parfait quand tu dois prouver qu'une équation du type f(x) = k admet une solution unique. Ça marche à tous les coups si tu respectes la méthode !
La technique est toujours la même : tu choisis un intervalle où ta fonction est continue et strictement monotone (croissante ou décroissante). Ensuite, tu vérifies que la valeur k que tu cherches se trouve bien entre les valeurs aux bornes.
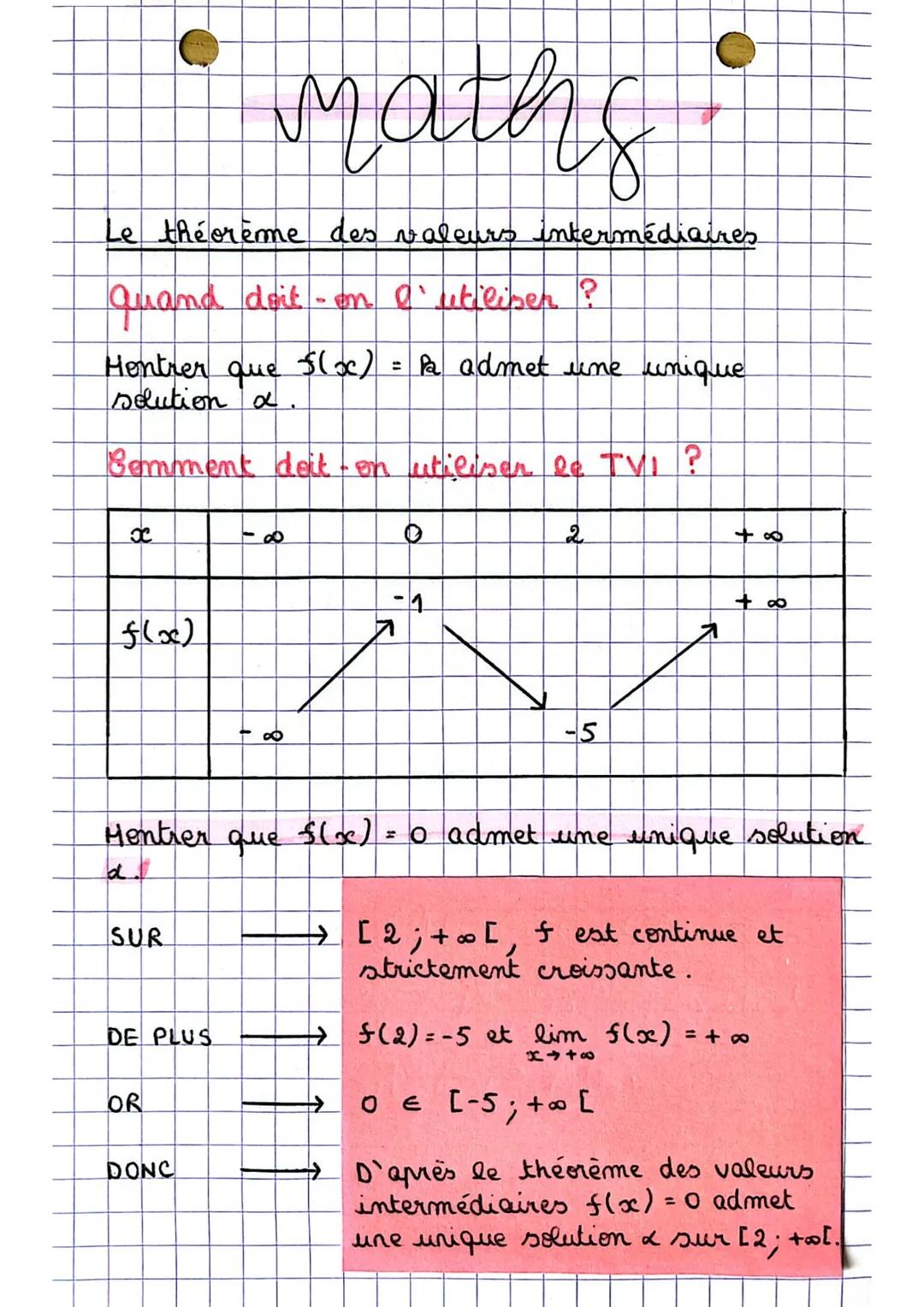
Prenons l'exemple concret : pour montrer que f(x) = 0 a une solution unique, on choisit l'intervalle [2; +∞[. Sur cet intervalle, f est continue et strictement croissante. On a f(2) = -5 et la limite en +∞ vaut +∞.
Astuce pratique : Vérifie toujours que 0 ∈ [-5; +∞[ avant d'appliquer le théorème. C'est cette condition qui garantit l'existence de ta solution !
Résultat : d'après le TVI, l'équation f(x) = 0 admet une unique solution sur [2; +∞[. Simple et efficace !