Applications et exemples pratiques
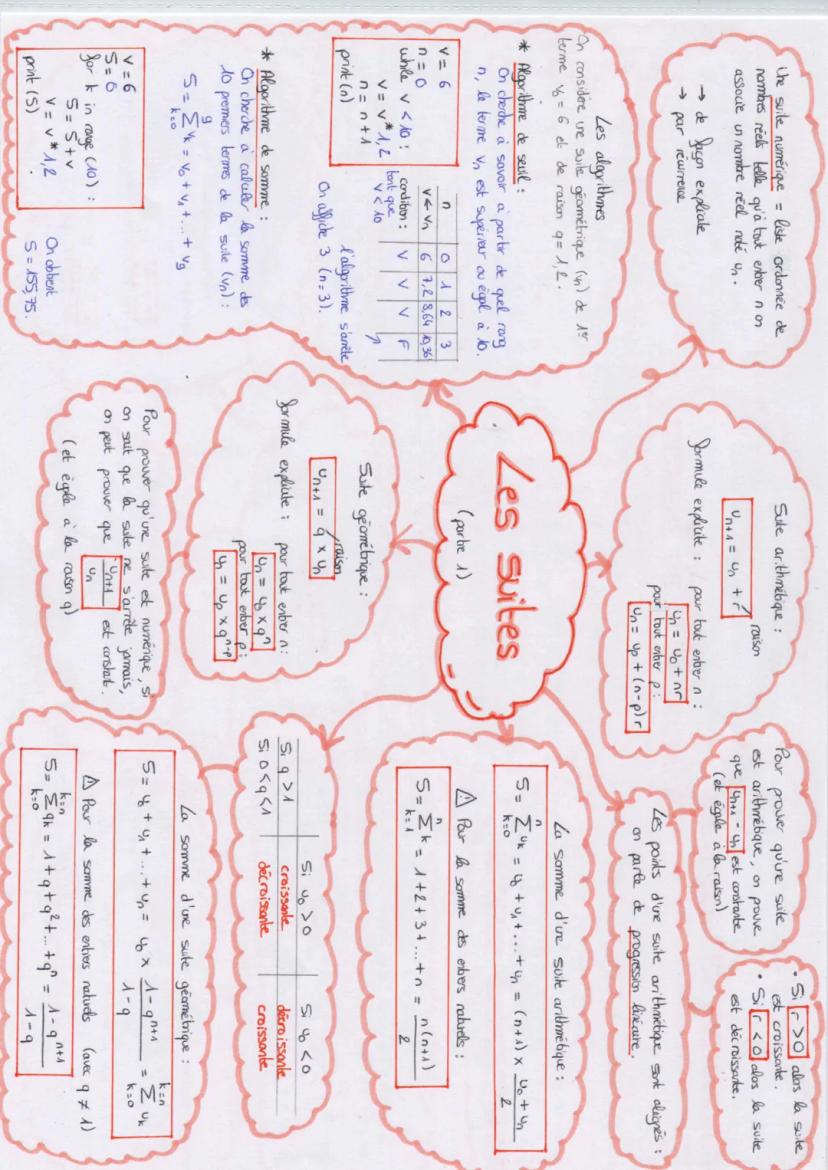
Les suites permettent de modéliser des évolutions dans le temps, comme le nombre de détenteurs d'un pass annuel. Par exemple, pour prévoir le nombre d'abonnés en 2030 avec une suite définie, on peut calculer u₍₁₄₎ = -3000×0,9^14 + 8000 ≈ 7059.
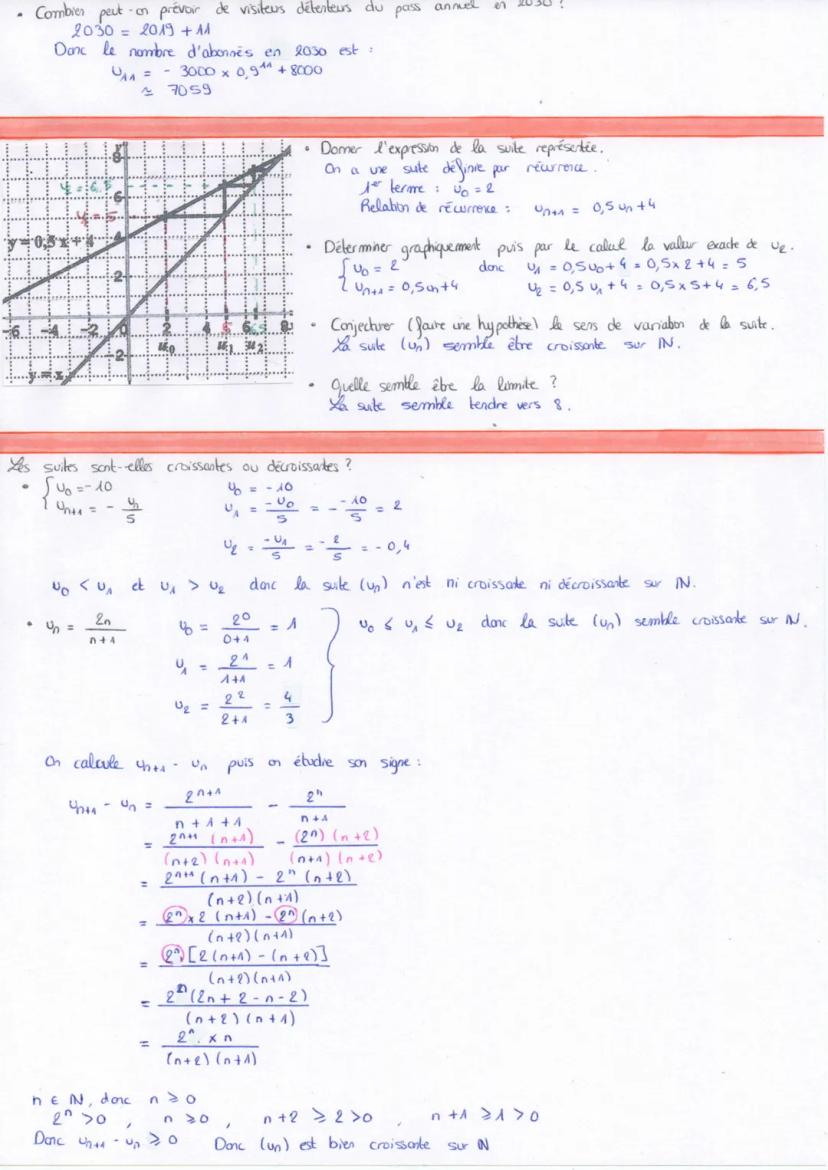
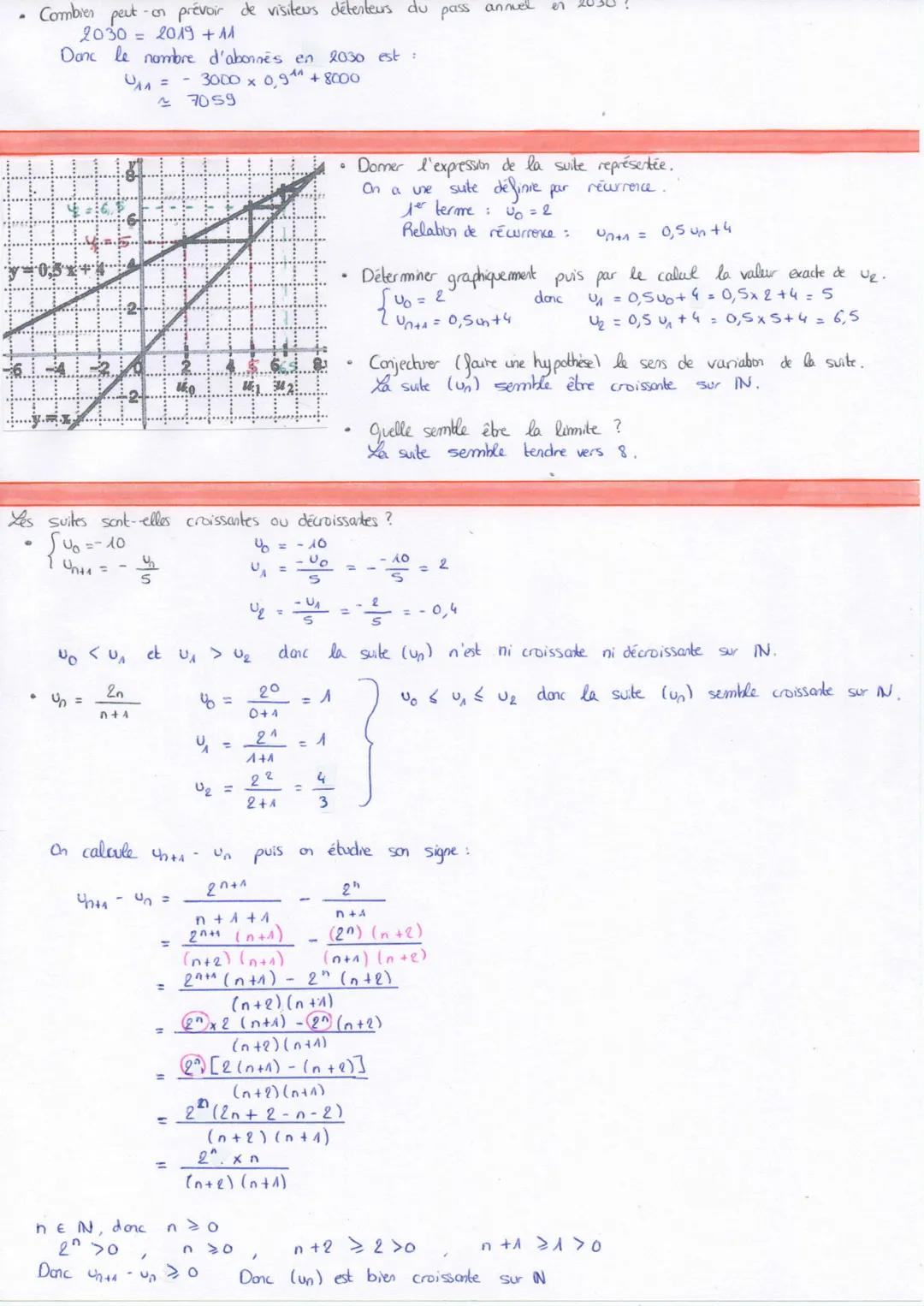
Pour étudier une suite définie par récurrence comme u₍₀₎ = 2 et u₍ₙ₊₁₎ = 0,5u₍ₙ₎ + 4, on calcule les premiers termes : u₍₁₎ = 5, u₍₂₎ = 6,5... On peut alors conjecturer que la suite est croissante et semble converger vers 8.
L'étude du sens de variation d'une suite est essentielle. Pour une suite définie par u₍ₙ₎ = 2^n/n+4, on calcule u₍ₙ₊₁₎ - u₍ₙ₎ et on étudie le signe de cette différence. Après simplification, on obtient une expression dont le signe permet de conclure sur la monotonie.
🔍 À retenir : Pour démontrer qu'une suite est monotone, calculez la différence entre deux termes consécutifs u(n+1)−u(n) et étudiez son signe. Si cette différence est toujours positive, la suite est croissante.
Certaines suites comme u₍₀₎ = -10 et u₍ₙ₊₁₎ = -√u(n)/5 ne sont ni croissantes ni décroissantes sur ℕ. Il faut alors calculer plusieurs termes consécutifs pour observer leur comportement : u₍₀₎ = -10, u₍₁₎ = 2, u₍₂₎ = -0,4.