Le discriminant et les racines
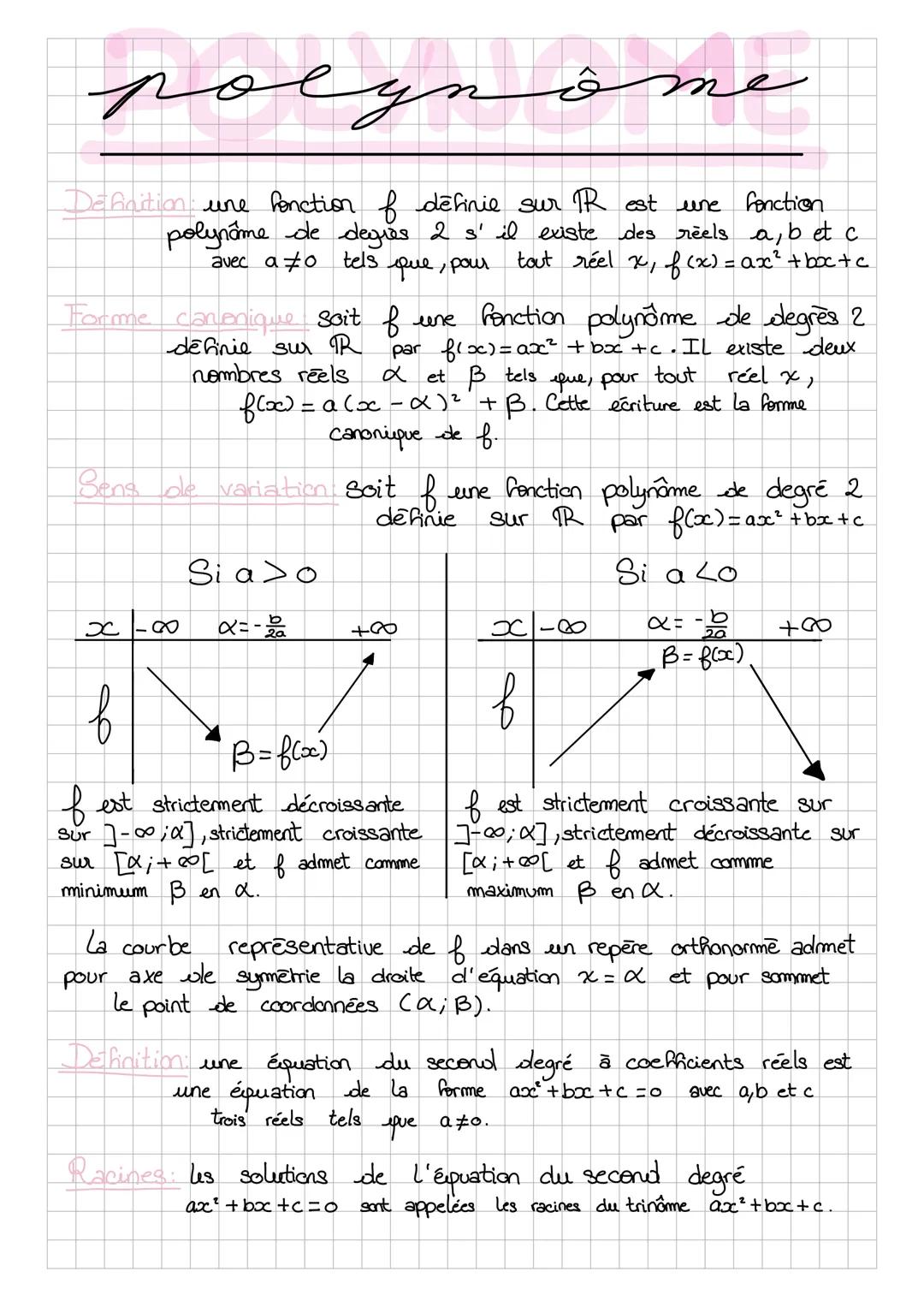
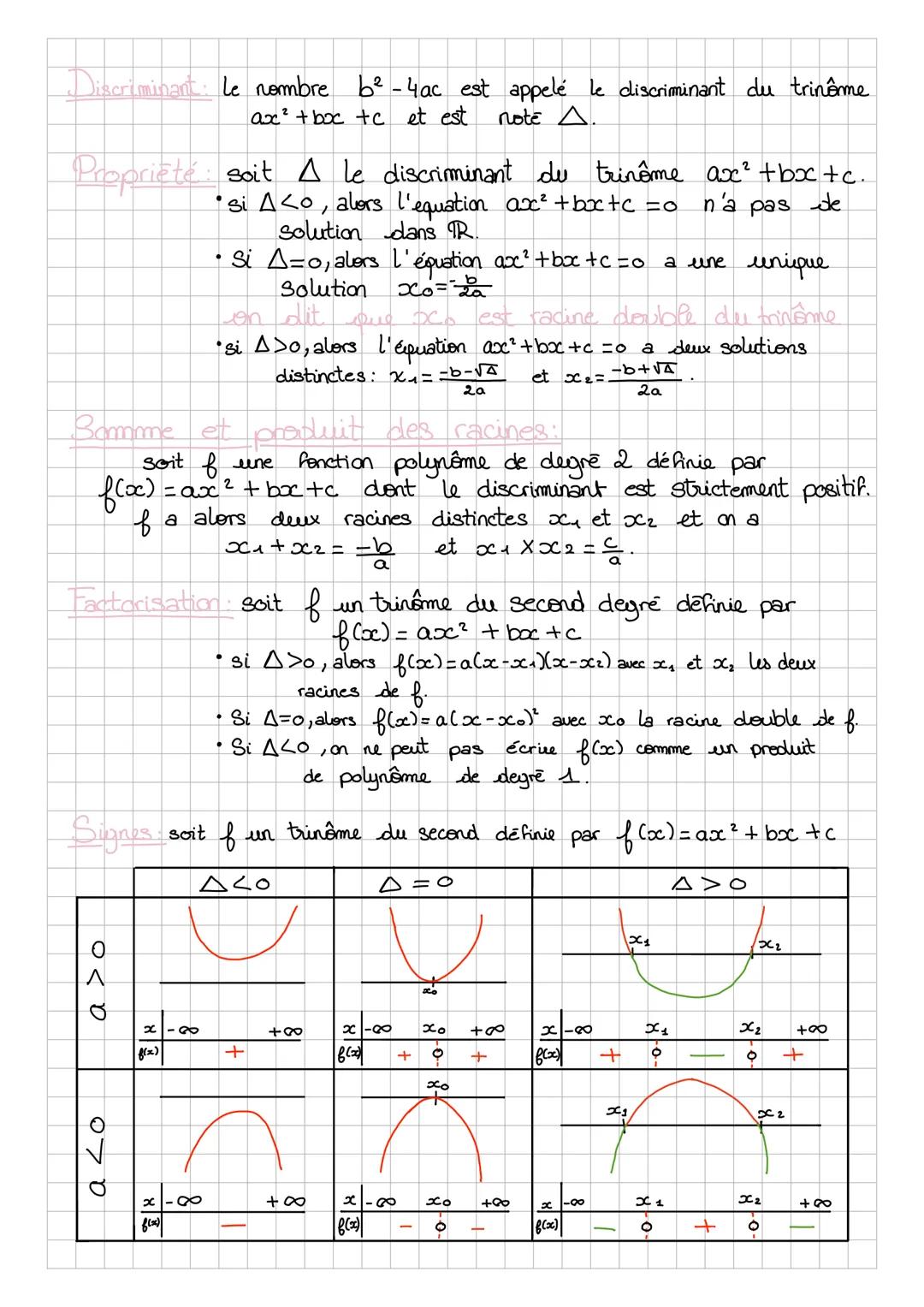
Le discriminant Δ = b² - 4ac est ton meilleur ami pour résoudre les équations du second degré ! Il te dit combien de solutions a ton équation ax² + bx + c = 0, qu'on appelle les racines du trinôme.
C'est simple à retenir : si Δ < 0, pas de solution réelle (ta parabole ne touche jamais l'axe des x). Si Δ = 0, une seule solution x₀ = -b/(2a) - on dit que c'est une racine double. Si Δ > 0, deux solutions distinctes avec les formules x₁ = −b−√Δ/(2a) et x₂ = −b+√Δ/(2a).
La factorisation découle directement du discriminant. Quand Δ > 0, tu peux écrire f(x) = ax−x1x−x2. Quand Δ = 0, ça donne f(x) = ax−x0². Et quand Δ < 0, impossible de factoriser avec des polynômes de degré 1 !
💡 Bonus : Les formules de somme et produit des racines x1+x2=−b/aetx1×x2=c/a peuvent te faire gagner du temps dans certains exercices !