Les Suites et Raisonnement par Récurrence

Le raisonnement par récurrence est une méthode puissante pour démontrer qu'une propriété est vraie pour tous les entiers naturels. Voici comment procéder :

1. Initialisation : Vérifier que P(0) est vraie
2. Hérédité : Supposer que P(n) est vraie et démontrer que P$n+1$ est également vraie
3. Conclusion : Si P(0) est vraie et P(n) est héréditaire, alors P(n) est vraie pour tout entier naturel

Pour les limites de suites, il faut déterminer la valeur vers laquelle une suite tend. Attention aux formes indéterminées : ∞-∞, 0×∞, ∞/∞, 0/0.

💡 Utilise le théorème des gendarmes : si une suite est encadrée entre deux suites qui tendent vers la même limite L, alors elle tend aussi vers L.

N'oublie pas le théorème de convergence monotone : une suite majorée et croissante (ou minorée et décroissante) converge toujours. Les fonctions cos(n) et sin(n) sont encadrées entre -1 et 1, ce qui peut être utile pour déterminer des limites.

Limites de Fonctions

Les limites de fonctions nous permettent de comprendre le comportement d'une fonction aux bornes de son domaine ou près d'un point particulier.

Si lim f(x) = L quand x→∞, alors la droite d'équation y = L est une asymptote horizontale de la courbe.

Si lim g(x) = ∞ quand x→a, alors la droite d'équation x = a est une asymptote verticale de la courbe.

Pour les limites en un réel a, on distingue :

• La limite à droite (x→a⁺)
• La limite à gauche (x→a⁻)

Méfie-toi des formes indéterminées : ∞-∞, 0×∞, ∞/∞, 0/0.

💡 Pour les croissances comparées, retiens la règle : "L'exponentielle l'emporte sur toute puissance" quand x tend vers l'infini.

Le théorème de comparaison est un outil essentiel : si deux fonctions se comportent de façon similaire au voisinage d'un point, leurs limites sont liées.

Dérivation, Continuité et Convexité

La tangente à une courbe au point A est la droite passant par A avec un coefficient directeur égal au nombre dérivé f'(a). Son équation est : y = f'(a)$x-a$ + f(a).

La dérivée nous renseigne sur le sens de variation d'une fonction :

• Si f'(x) > 0, alors f est croissante
• Si f'(x) < 0, alors f est décroissante

Quelques dérivées essentielles :

• $x^n$' = nx^$n-1$
• $1/x^n$' = -n/x^$n+1$
• $e^x$' = e^x
• (u×v)' = u'v + uv'
• $u/v$' = $u'v - uv'$/v²

💡 Le théorème des valeurs intermédiaires est crucial : si f est continue sur [a;b], alors f prend toutes les valeurs entre f(a) et f(b).

Pour la convexité, observe le signe de la dérivée seconde :

• Si f''(x) < 0, la fonction est concave
• Si f''(x) > 0, la fonction est convexe
• Si f''(x) = 0, on peut avoir un point d'inflexion

Combinaison et Dénombrement

Un ensemble E est une collection d'objets distincts appelés éléments. Le nombre d'éléments de E est noté card(E).

Pour deux ensembles E et F disjoints :

• card(E×F) = card(E)×card(F) (principe multiplicatif)
• card(E∪F) = card(E) + card(F) (principe additif)

Si E et F ne sont pas disjoints : card(E∪F) = card(E) + card(F) - card(E∩F)

Un k-uplet est une collection ordonnée de k éléments de E. Si card(E) = m, il y a m^k k-uplets possibles.

💡 Les arrangements sont des k-uplets d'éléments distincts. Leur nombre est A(m,k) = m!/$m-k$!. L'ordre compte !

Une permutation est un arrangement de tous les éléments $k = m$. Il y a m! permutations.

Une combinaison est un sous-ensemble de k éléments choisis parmi m. Il y a C(m,k) = m!/$k!(m-k)!$ combinaisons possibles. L'ordre n'importe pas !

Retiens la relation : Combinaison × Permutation = Arrangement

Binômes et Triangle de Pascal

Les coefficients binomiaux C(n,k) (notation binomiale) possèdent plusieurs propriétés importantes :

La propriété de symétrie : C(n,k) = C$n,n-k$ pour tout k tel que 0 ≤ k ≤ n.

La propriété du triangle de Pascal : C(n,k) = C$n-1,k-1$ + C$n-1,k$ pour tout n et k tels que 0 < k < n.

Le triangle de Pascal est une représentation visuelle de ces coefficients :

1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1

💡 La somme des coefficients binomiaux d'une ligne n du triangle est égale à 2^n : C(n,0) + C(n,1) + ... + C(n,n) = 2^n

Cette propriété représente le nombre total de sous-ensembles possibles d'un ensemble à n éléments.

Vecteurs, Droites et Plans dans l'Espace

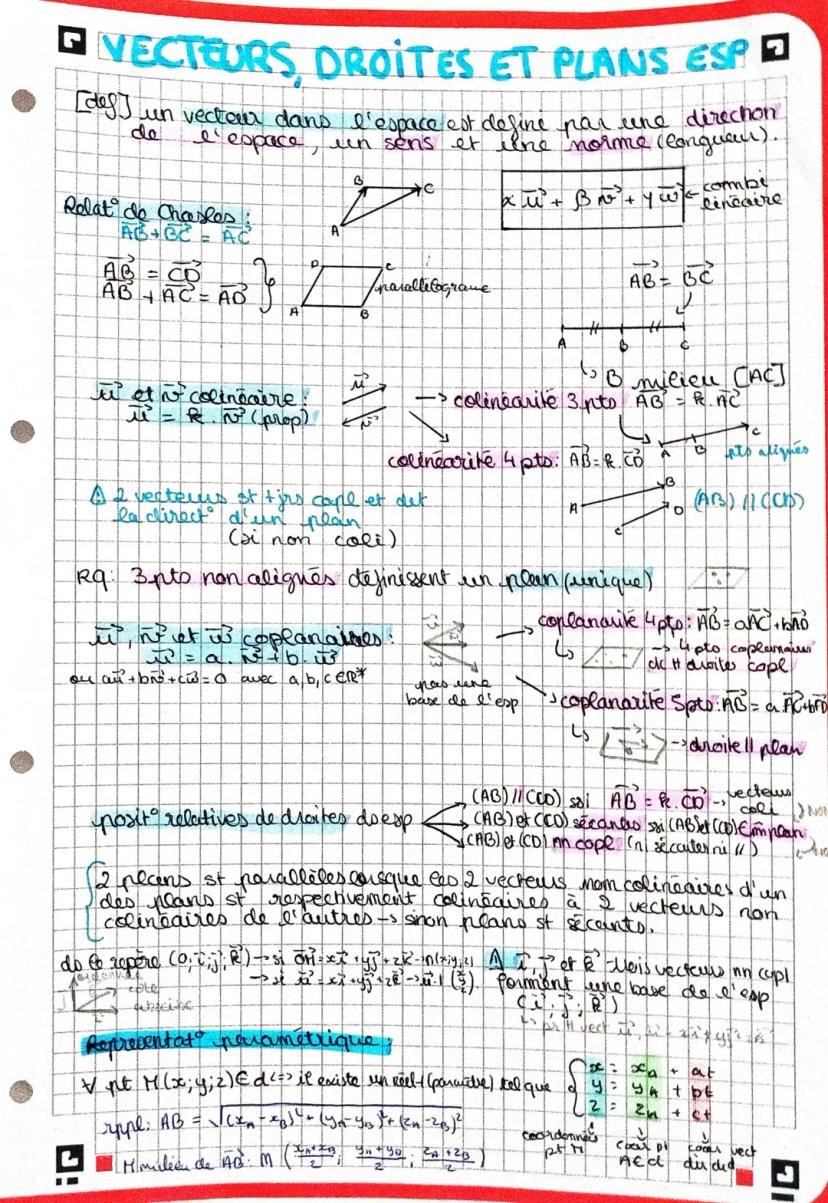
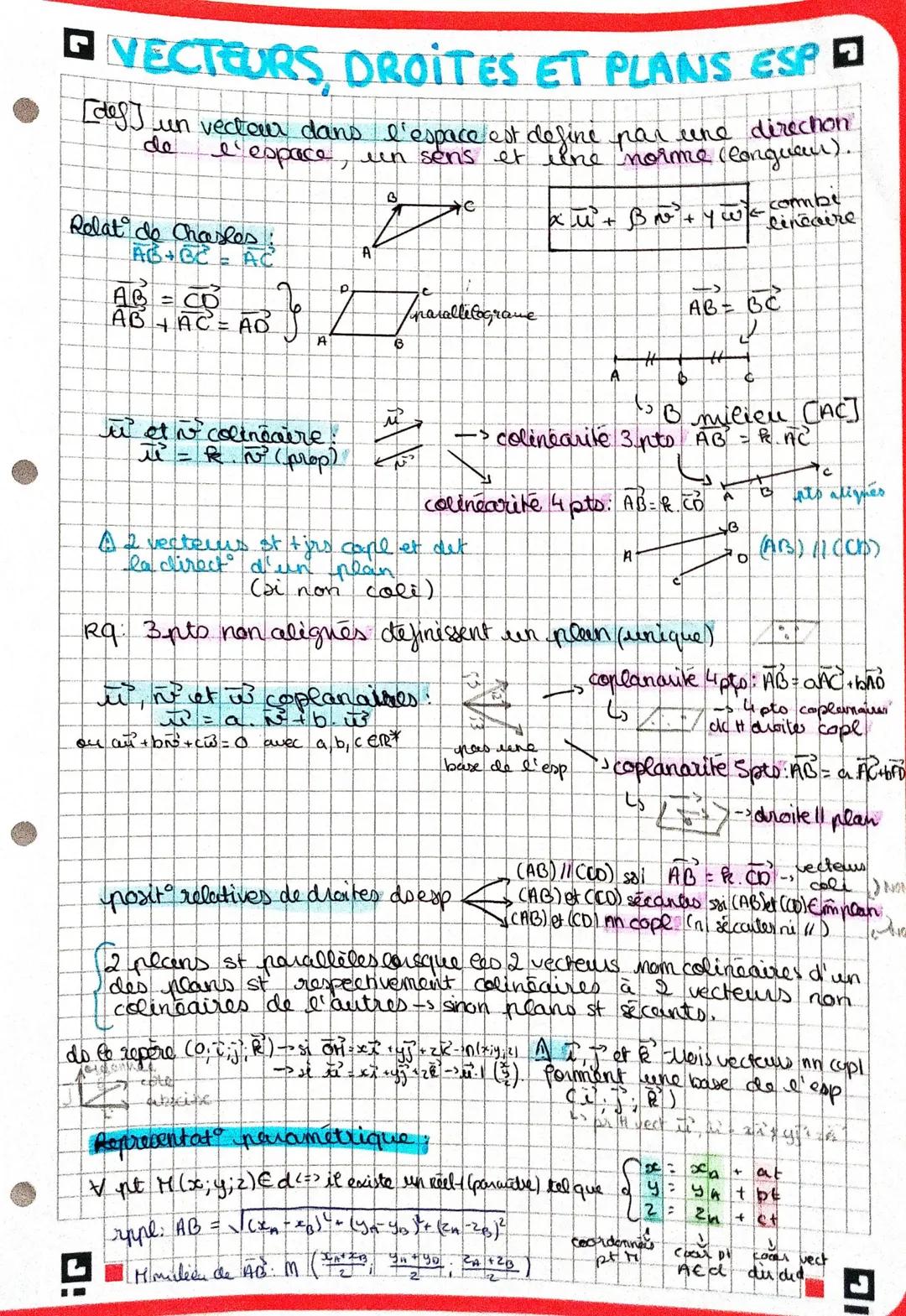
Un vecteur dans l'espace est défini par une direction, un sens et une norme (longueur).

La relation de Chasles nous donne : AB + BC = AC

Deux vecteurs sont colinéaires s'il existe un réel k tel que u = k×v.

Trois points non alignés définissent un plan unique. Deux vecteurs non colinéaires définissent la direction d'un plan.

Trois vecteurs sont coplanaires s'il existe des réels a, b, c non tous nuls tels que au + bv + cw = 0.

💡 Pour vérifier la coplanarité de 4 points, on vérifie s'il existe α et β tels que AB = αAC + βAD.

Positions relatives des droites et plans dans l'espace :

• Deux plans sont parallèles si leurs vecteurs normaux sont colinéaires
• Deux droites peuvent être : parallèles, sécantes ou non coplanaires

Dans un repère (O, i, j, k), un point M a pour coordonnées (x,y,z).

La représentation paramétrique d'une droite : M(x,y,z) ∈ d ⟺ il existe un réel t tel que les coordonnées suivent une relation linéaire.

Fonction Logarithme Népérien

Le logarithme népérien d'un réel strictement positif a, noté ln(a), est l'unique solution de l'équation e^x = a.

La fonction ln est définie sur ]0;+∞[ → ℝ et vérifie :

• e^(ln(a)) = a
• ln$e^a$ = a

Les fonctions exp et ln sont réciproques l'une de l'autre. Leurs courbes sont symétriques par rapport à la droite y = x.

Propriétés essentielles :

• ln(xy) = ln(x) + ln(y)
• ln$x/y$ = ln(x) - ln(y)
• ln$x^r$ = r×ln(x)

💡 La dérivée du logarithme est (ln(x))' = 1/x et celle d'une composée est (ln(u(x)))' = u'(x)/u(x), avec u(x) > 0.

ln(x) est strictement croissante et concave sur ]0;+∞[.

Limites importantes :

• lim ln(x) = -∞ quand x → 0
• lim ln(x) = +∞ quand x → +∞
• lim ln(x)/x = 0 quand x → +∞
• lim x^n×ln(x) = 0 quand x → 0, pour tout n > 0

Loi Binomiale

Une expérience de Bernoulli est une expérience à deux issues : "succès" (probabilité p) et "échec" $probabilité 1-p$.

Pour une variable aléatoire X suivant la loi de Bernoulli de paramètre p :

• E(X) = p (espérance)
• V(X) = p$1-p$ (variance)

La loi binomiale B(n,p) modélise le nombre de succès dans n épreuves de Bernoulli identiques et indépendantes.

Pour une variable X suivant B(n,p) :

• P$X = k$ = C(n,k) × p^k × $1-p$^$n-k$
• E(X) = n×p
• V(X) = n×p×$1-p$
• σ(X) = √$n×p×(1-p)$

💡 Sur la calculatrice, utilise "binomFdp" pour P$X = k$ et "binomFrép" pour P(X ≤ k). Pour P(X ≥ a), calcule 1 - P$X ≤ a-1$.

Pour calculer une probabilité dans un intervalle : P(a ≤ X ≤ b) = P(X ≤ b) - P$X ≤ a-1$.

Orthogonalité dans l'Espace

Le produit scalaire de deux vecteurs u et v est noté u·v.

Deux vecteurs sont orthogonaux si leur produit scalaire est nul : u·v = 0.

Propriétés importantes du produit scalaire :

• u·v = ||u|| × ||v|| × cos(u,v)
• Si u et v sont de même sens, alors u·v = ||u|| × ||v||
• Si u et v sont de sens contraires, alors u·v = -||u|| × ||v||

En coordonnées : u·v = x₁x₂ + y₁y₂ + z₁z₂

💡 Un vecteur n non nul est normal à un plan P s'il est vecteur directeur d'une droite orthogonale au plan.

L'équation cartésienne d'un plan est de la forme ax + by + cz + d = 0, où (a,b,c) sont les coordonnées d'un vecteur normal au plan.

Le plan médiateur d'un segment [AB] est le plan passant par le milieu I de [AB] et de vecteur normal AB.

Le projeté orthogonal d'un point A sur une droite d est le point H tel que H ∈ d et (AH) ⊥ d.

Primitives et Équations Différentielles

Une primitive d'une fonction f sur un intervalle I est une fonction F telle que F' = f.

Quelques primitives essentielles :

• x^n → x^$n+1$/$n+1$ + C $pour n ≠ -1$
• 1/x → ln|x| + C
• e^x → e^x + C
• cos(x) → sin(x) + C
• sin(x) → -cos(x) + C

Pour résoudre les équations différentielles du premier ordre :

1. Pour y' = ay :

   • Les solutions sont de la forme y = Ke^(ax)
   • Exemple : y' + 5y = 0 a pour solutions y = Ke^$-5x$

2. Pour y' = ay + b :

   • Les solutions sont de la forme y = Ke^(ax) - b/a
   • Exemple : y' = 3y + 1 a pour solutions y = Ke^(3x) - 1/3

💡 Pour résoudre une équation différentielle y' = ay + f(x), cherche d'abord une solution particulière puis ajoute les solutions de l'équation homogène y' = ay.

3. Pour y' = ay + f(x) :
   • Les solutions sont de la forme y = Ke^(ax) + u(x), où u est une solution particulière