Propriétés générales des paraboles
Avec f(x) = -2x² + 4x + 3, tu vois l'effet d'un coefficient a négatif. La parabole est maintenant tournée vers le bas, et le sommet correspond au maximum de la fonction.
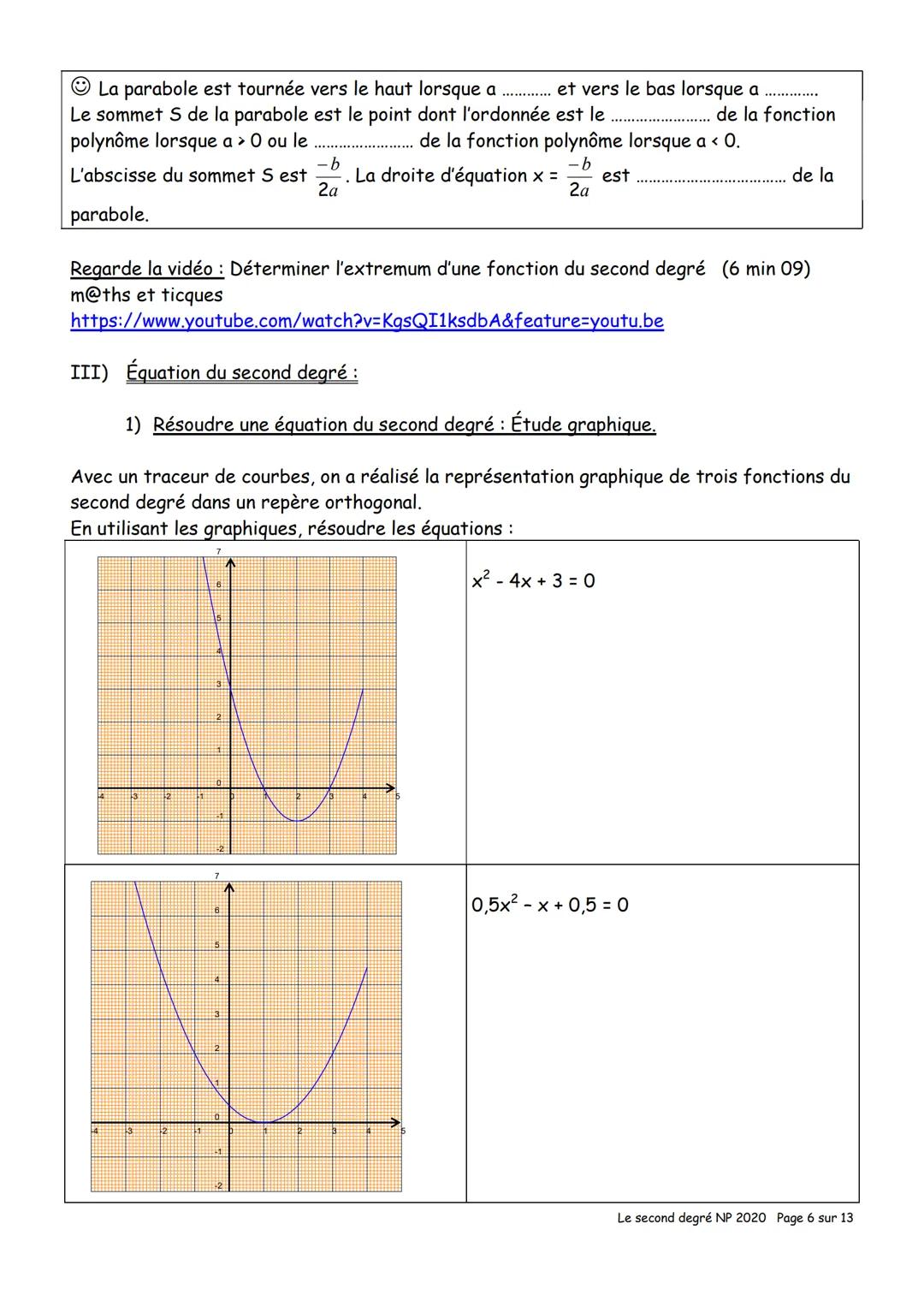
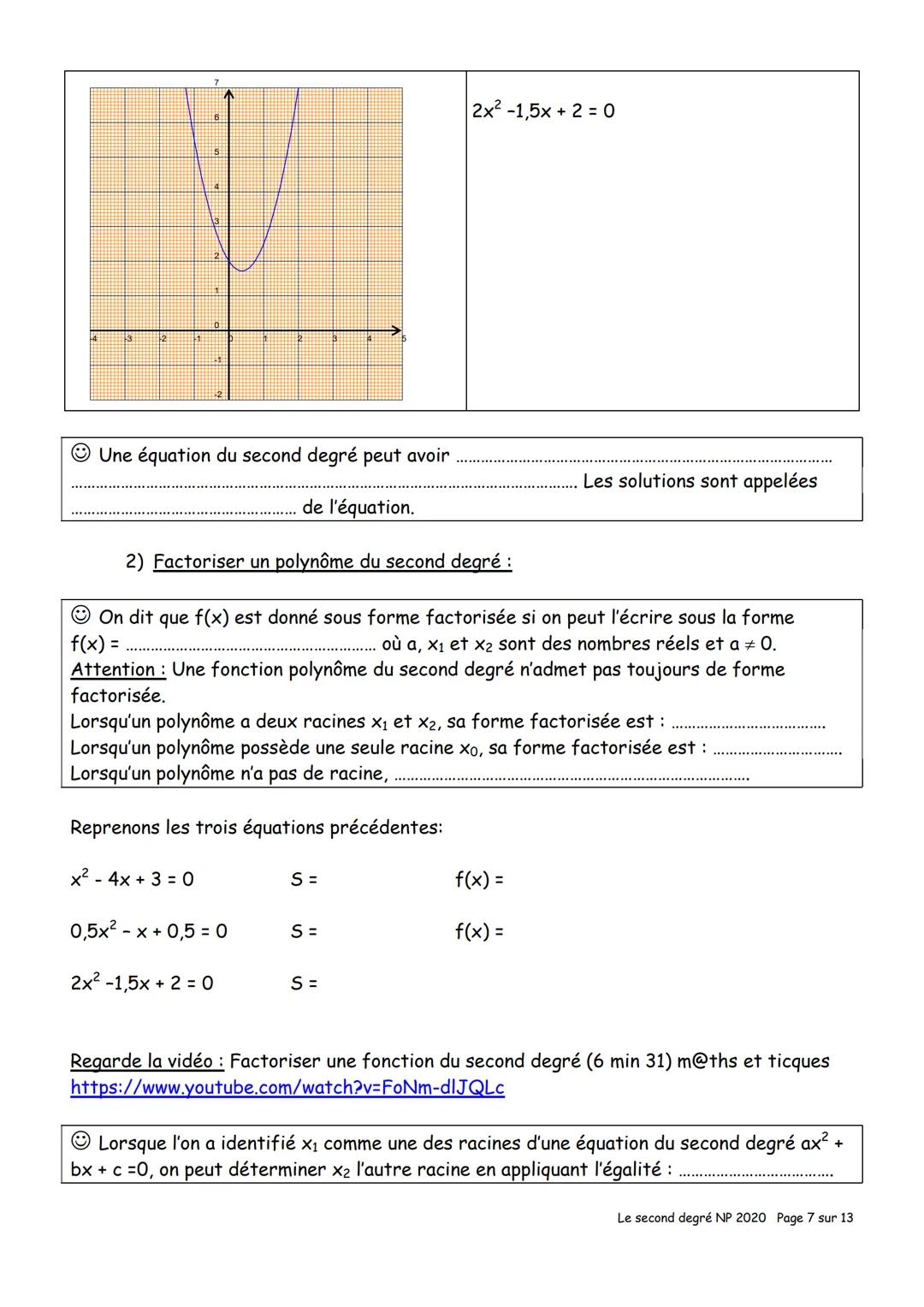
La formule du sommet est universelle : l'abscisse du sommet vaut toujours -b/(2a). Dans f(x) = ax² + bx + c, identifie les valeurs de a et b, puis applique cette formule.
Compare tes résultats : pour f(x) = x² - 5x + 2, tu as a = 1, b = -5, donc -b/(2a) = 5/2 = 2,5. Pour f(x) = -2x² + 4x + 3, tu as a = -2, b = 4, donc -b/(2a) = -4/(-4) = 1.
⚡ Règle d'or : La droite x = -b/(2a) est l'axe de symétrie de ta parabole. Tout ce qui se passe à droite de cette droite se répète symétriquement à gauche !