Le discriminant et les solutions
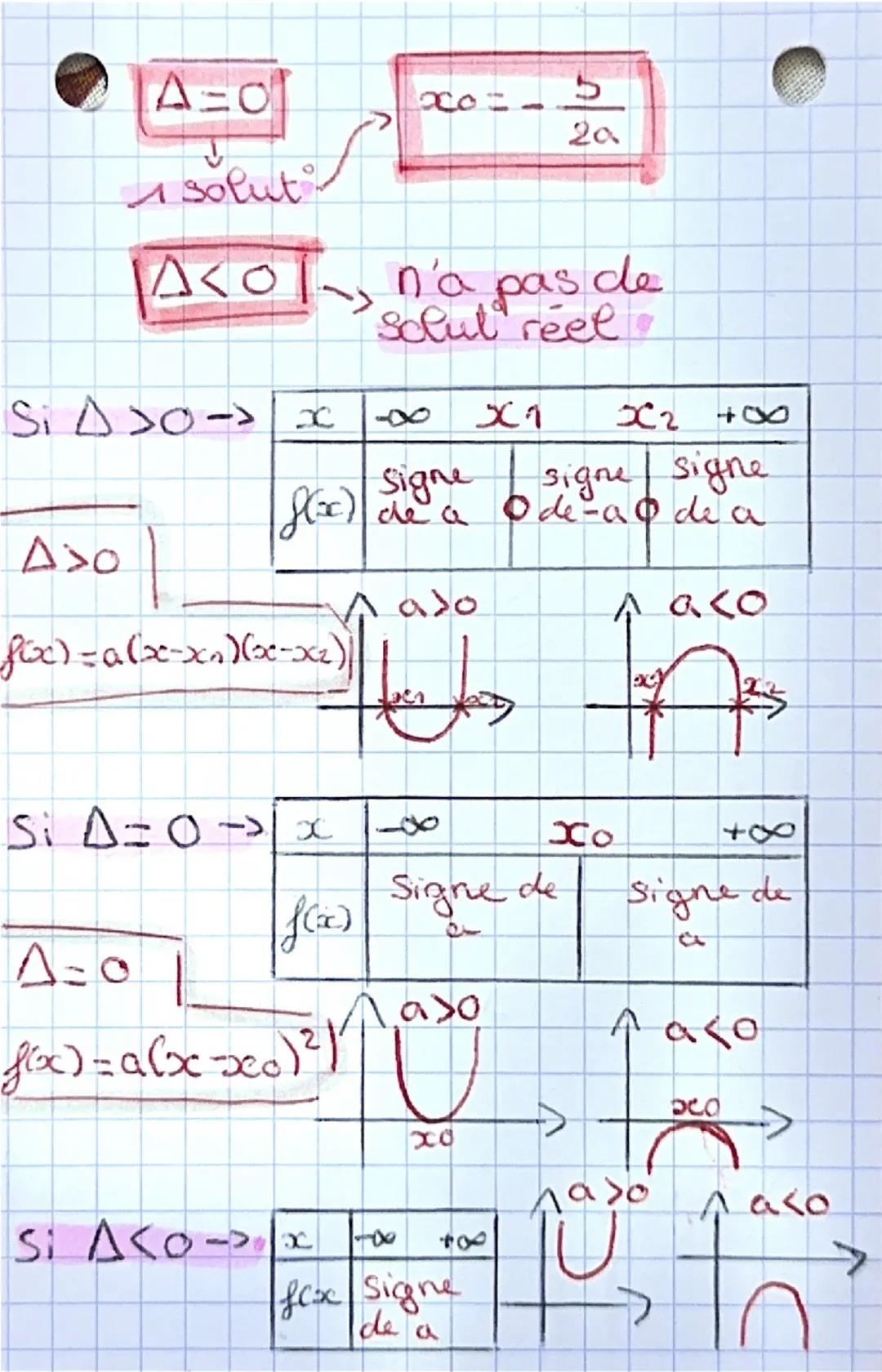
Le discriminant Δ=b2−4ac te dit exactement combien de fois ta parabole coupe l'axe des abscisses. C'est l'outil magique pour résoudre tes équations du second degré sans te tromper.
Quand Δ>0, tu as deux solutions distinctes x1 et x2, et ta fonction s'écrit f(x)=a(x−x1)(x−x2). Si Δ=0, une seule solution x0 existe, donnant f(x)=a(x−x0)2.
Lorsque Δ<0, aucune solution réelle n'existe - ta parabole ne touche jamais l'axe des x. Dans ce cas, le signe de la fonction est toujours celui de a.
🎯 À retenir : Le discriminant détermine le nombre de racines, et le coefficient a détermine le signe de la fonction entre les racines !