Suites arithmétiques
Une suite arithmétique, c'est quand tu ajoutes toujours la même constante pour passer d'un terme au suivant. Cette constante s'appelle la raison r, et on a un+1 = u(n) + r.
La raison r détermine complètement le comportement : si r > 0, la suite monte ; si r < 0, elle descend ; si r = 0, elle reste constante. C'est aussi simple que ça !
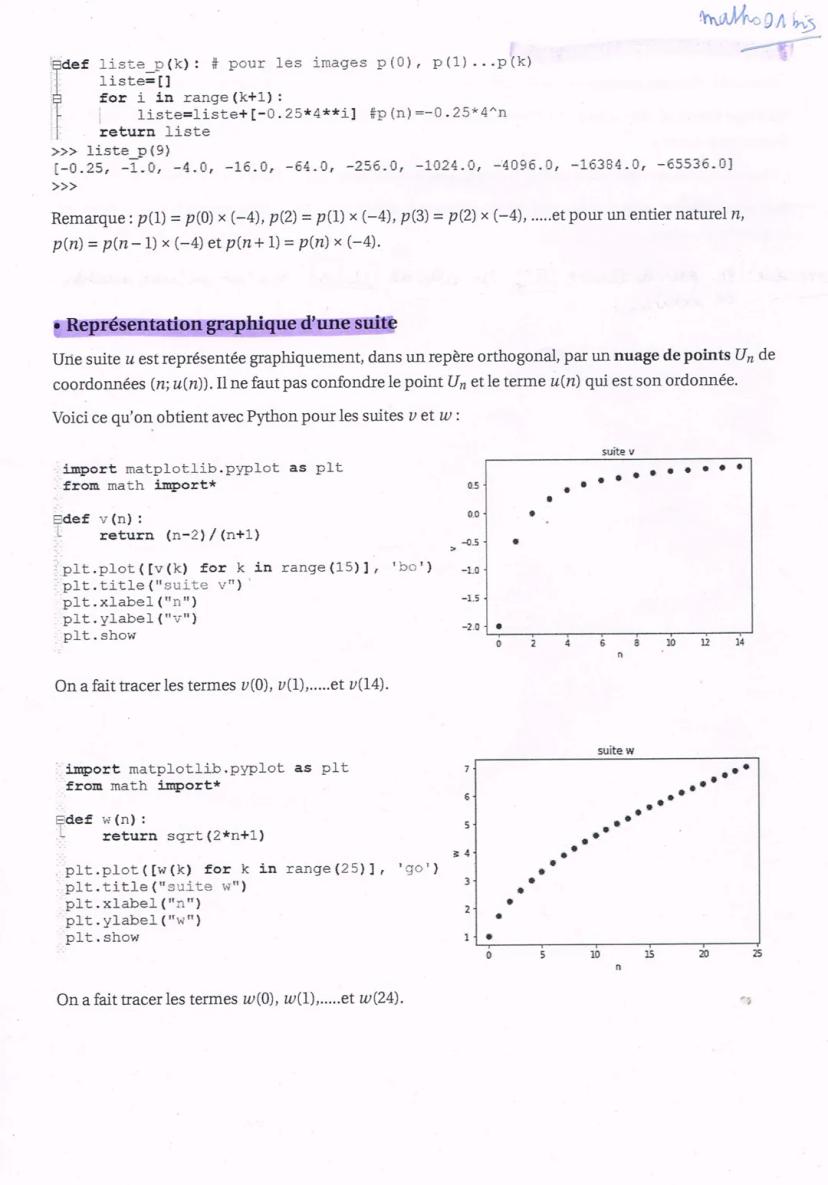
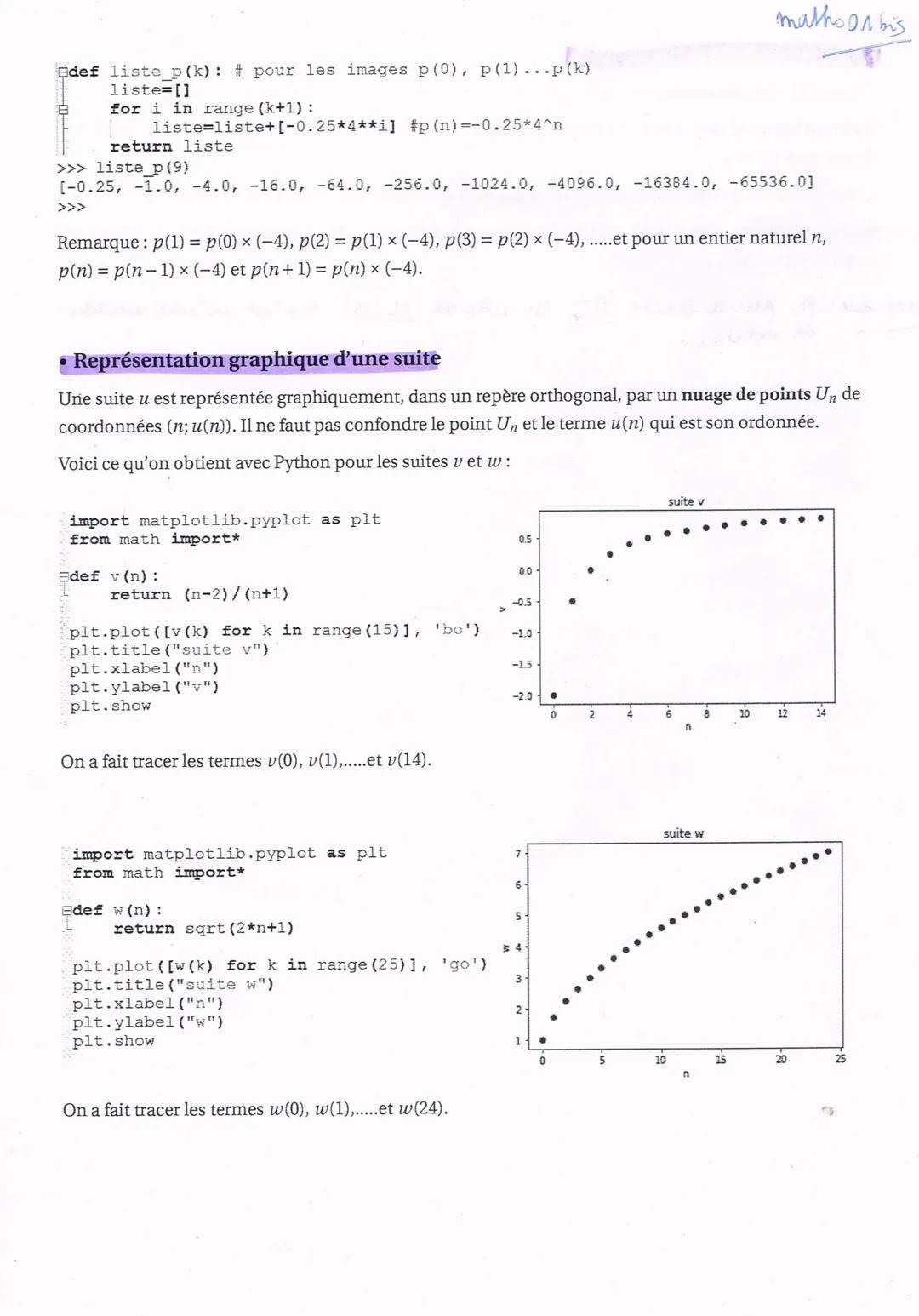
Graphiquement, une suite arithmétique forme toujours des points alignés. C'est même réciproque : si tes points sont alignés, ta suite est arithmétique ! La formule explicite est u(n) = u(0) + nr, qui correspond à une fonction affine.
Reconnaissance rapide : Points alignés = suite arithmétique. C'est un test visuel infaillible !