Les bases de la trigonométrie
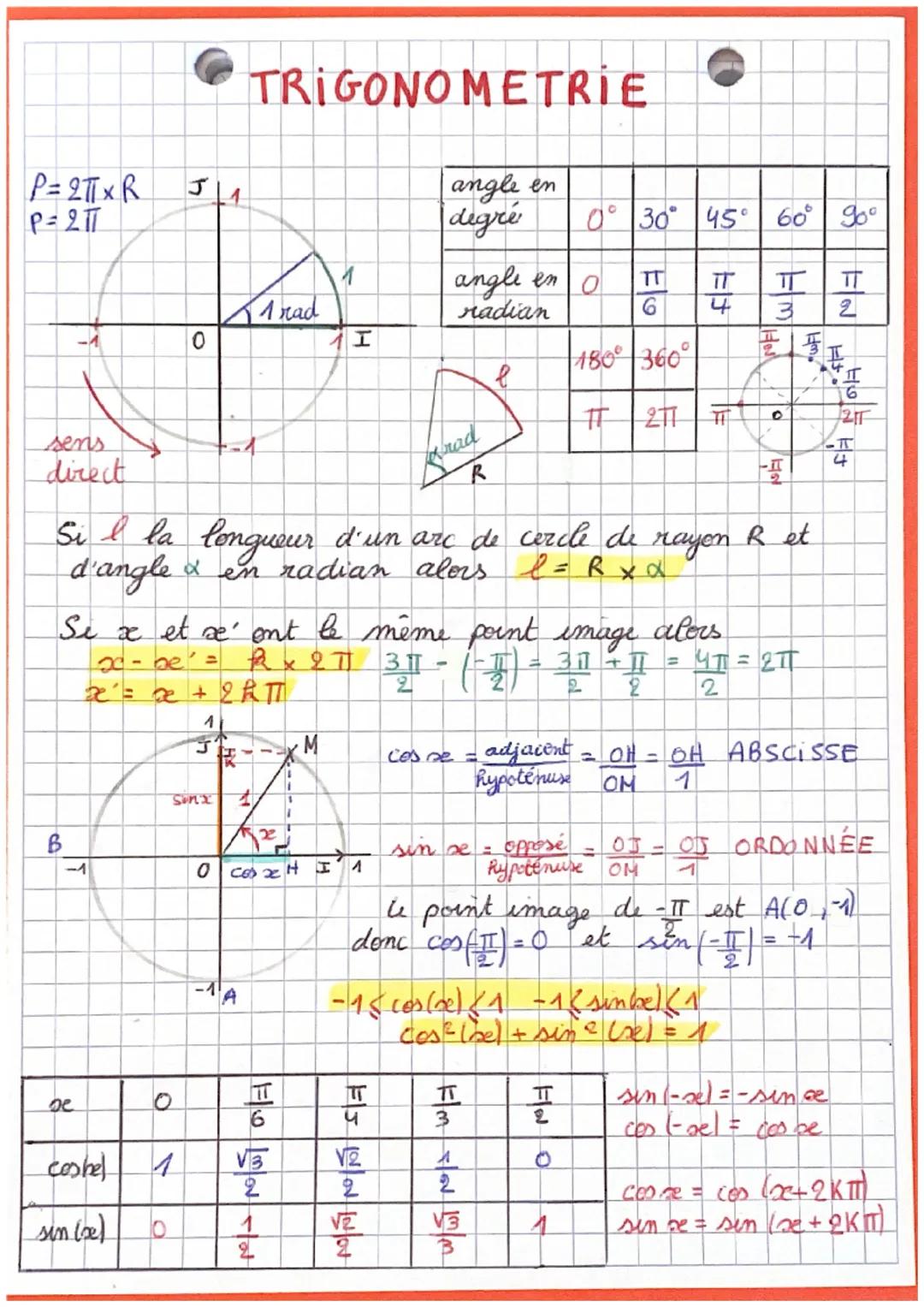
Tu sais déjà que le périmètre d'un cercle vaut P = 2πR, mais en trigo, on travaille surtout avec les angles en radians. C'est juste une autre façon de mesurer les angles, plus pratique que les degrés pour les calculs.
La conversion est simple : 180° = π radians. Donc 90° = π/2, 60° = π/3, 45° = π/4, et 30° = π/6. Retiens ces valeurs, tu les reverras partout !
La longueur d'un arc de cercle se calcule avec l = R × α (où α est en radians). Et si deux angles ont le même point sur le cercle trigonométrique, ils diffèrent de 2π : x' = x + 2kπ.
Les fonctions trigonométriques cos et sin représentent les coordonnées d'un point sur le cercle. cos x donne l'abscisse (coordonnée horizontale) et sin x l'ordonnée (coordonnée verticale). C'est pour ça qu'on a toujours -1 ≤ cos(x) ≤ 1 et -1 ≤ sin(x) ≤ 1.
Astuce : La relation fondamentale cos²(x) + sin²(x) = 1 est ton meilleur ami - elle te sauvera dans plein d'exercices !
Les propriétés importantes à retenir : sin−x = -sin(x) (fonction impaire), cos−x = cos(x) (fonction paire), et les deux fonctions sont périodiques avec une période de 2π.