Arithmétique - Division euclidienne et nombres premiers
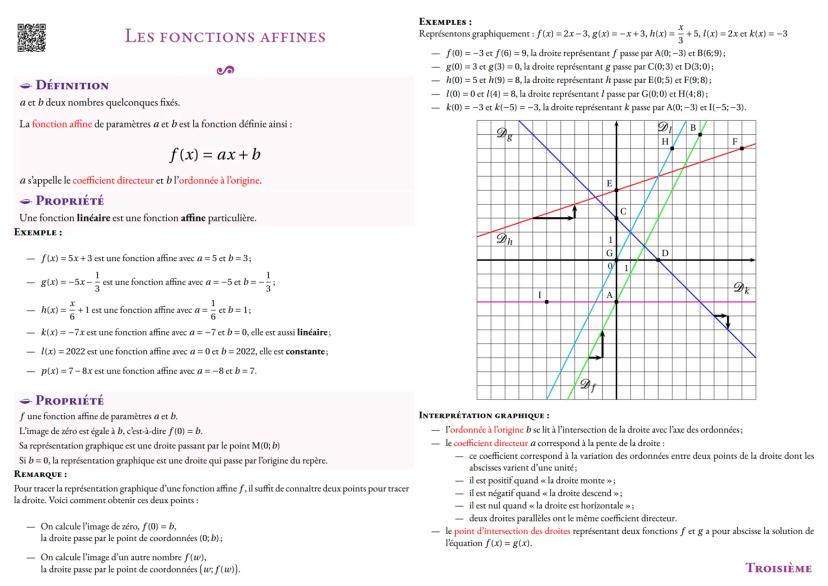
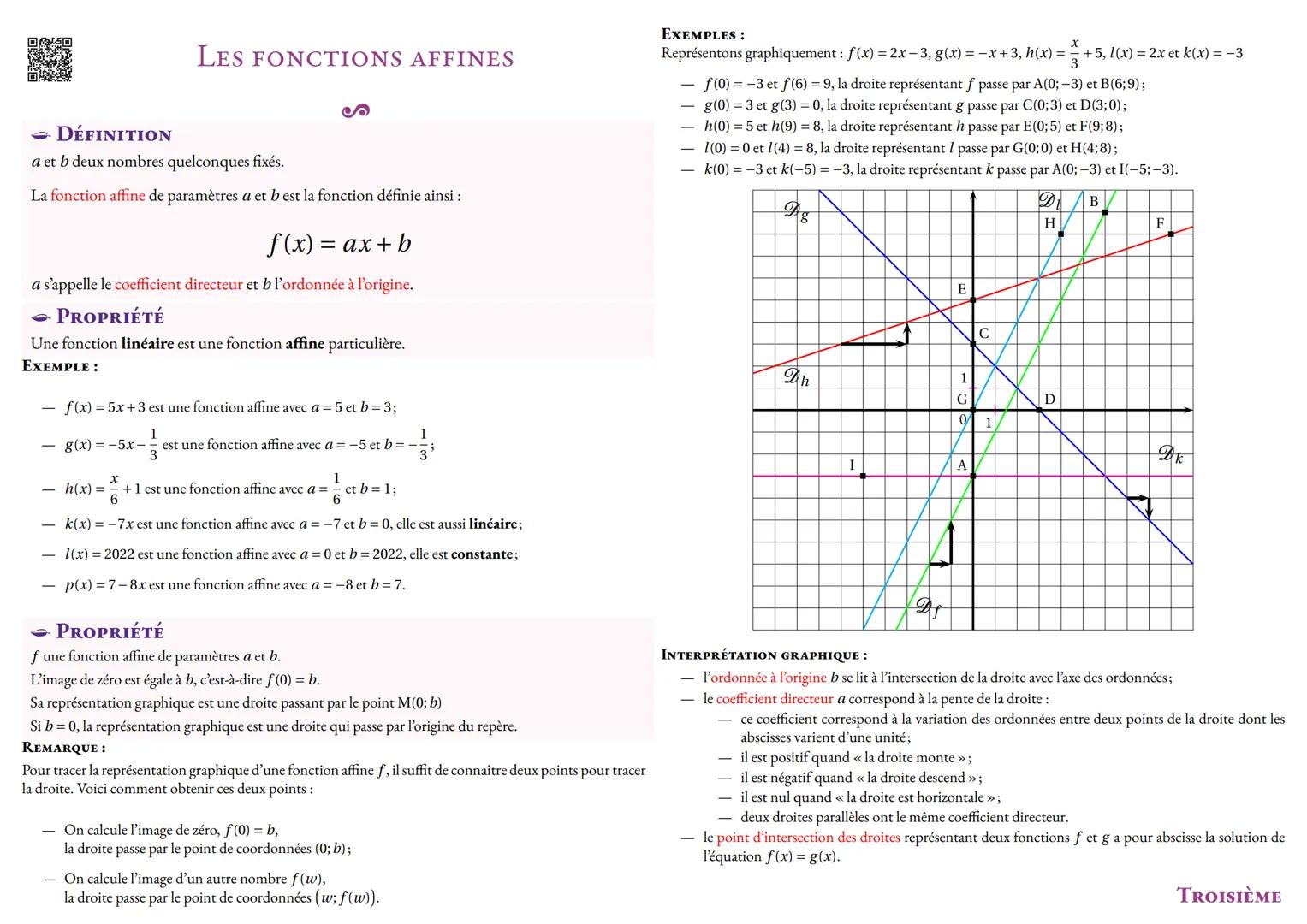
Tu sais déjà diviser, mais la division euclidienne te donne une méthode précise pour tout nombre. Quand tu divises a par b, tu obtiens toujours a = b × q + r, où q est le quotient et r le reste (toujours plus petit que b).
Les nombres premiers sont les "briques" de tous les nombres entiers. Un nombre premier n'a que deux diviseurs : 1 et lui-même. Attention, 1 n'est pas premier ! Les premiers nombres premiers sont 2, 3, 5, 7, 11, 13...
La décomposition en facteurs premiers te permet d'écrire n'importe quel nombre comme un produit de nombres premiers. Par exemple, 360 = 2³ × 3² × 5. Cette technique est super utile pour simplifier les fractions et trouver des diviseurs communs.
💡 Astuce : Pour vérifier qu'un nombre est divisible par 3, additionne tous ses chiffres - si le résultat est divisible par 3, le nombre l'est aussi !