Les bases des probabilités
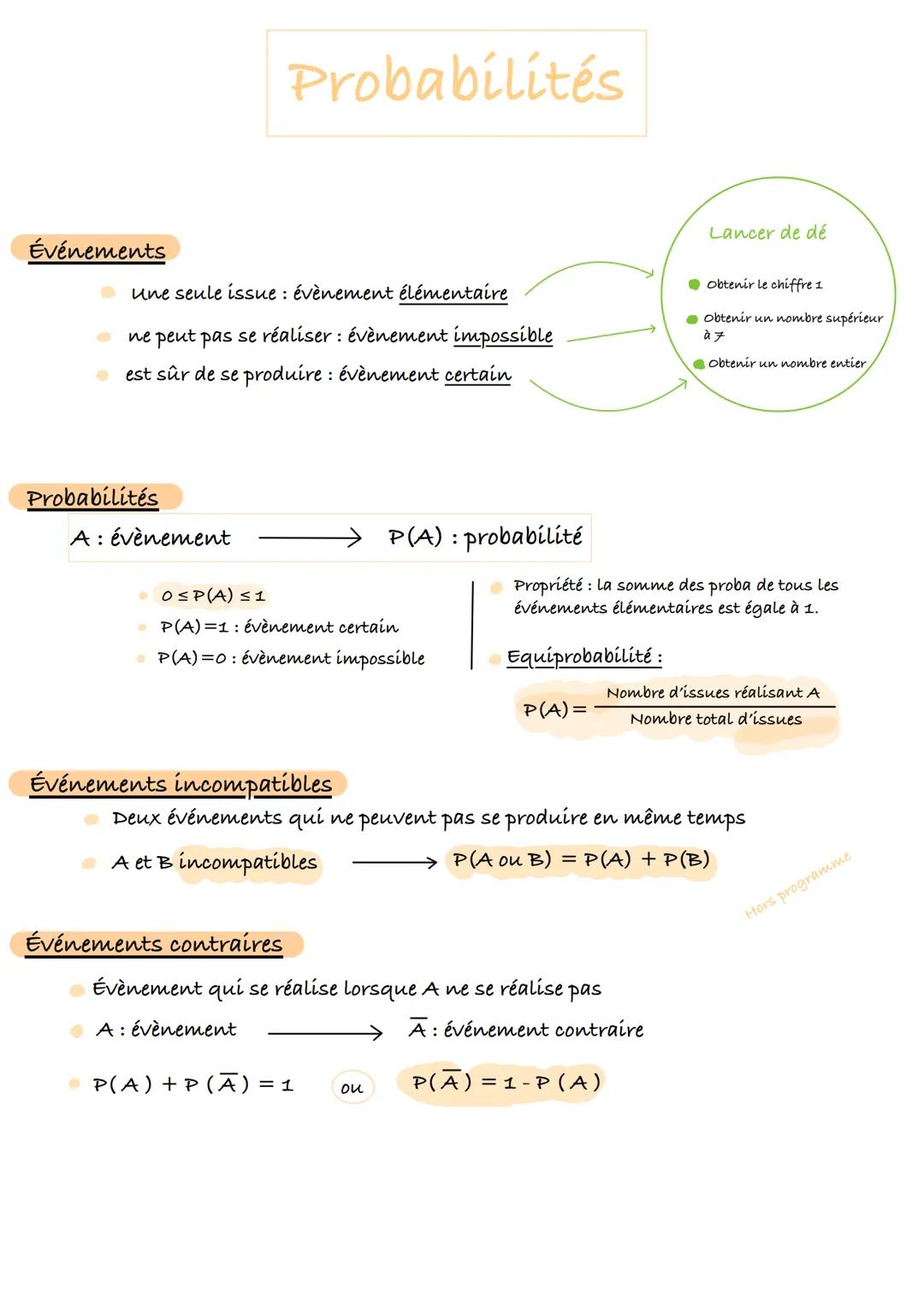
Imagine que tu lances un dé : chaque résultat possible s'appelle un événement élémentaire. Parfois, un événement est impossible (comme obtenir 8 avec un dé normal) ou certain (comme obtenir un nombre entre 1 et 6).
La probabilité d'un événement A s'écrit P(A) et c'est toujours un nombre entre 0 et 1. Si P(A) = 0, l'événement est impossible ; si P(A) = 1, il est certain de se produire.
Voici la formule magique pour calculer une probabilité : P(A) = Nombre d'issues favorables / Nombre total d'issues. Par exemple, la probabilité d'obtenir un 3 avec un dé est 1/6.
Astuce pratique : La somme de toutes les probabilités possibles égale toujours 1 !
Événements spéciaux
Deux types d'événements sont super importants à retenir. Les événements incompatibles ne peuvent jamais arriver en même temps (comme obtenir 2 ET 5 en un seul lancer). Dans ce cas : P(A ou B) = P(A) + P(B).
Les événements contraires sont encore plus cool ! L'événement contraire de A noté $\overline{A}$ se produit quand A ne se produit pas. Par exemple, si A = "obtenir un nombre pair", alors A = "obtenir un nombre impair".
La formule clé à retenir : P(A) + P$\overline{A}$ = 1, ou encore P$\overline{A}$ = 1 - P(A). C'est super pratique pour calculer rapidement certaines probabilités !
Conseil d'expert : Utilise les événements contraires quand il's plus facile de calculer ce qui NE va PAS arriver !