Les suites géométriques - L'essentiel à retenir
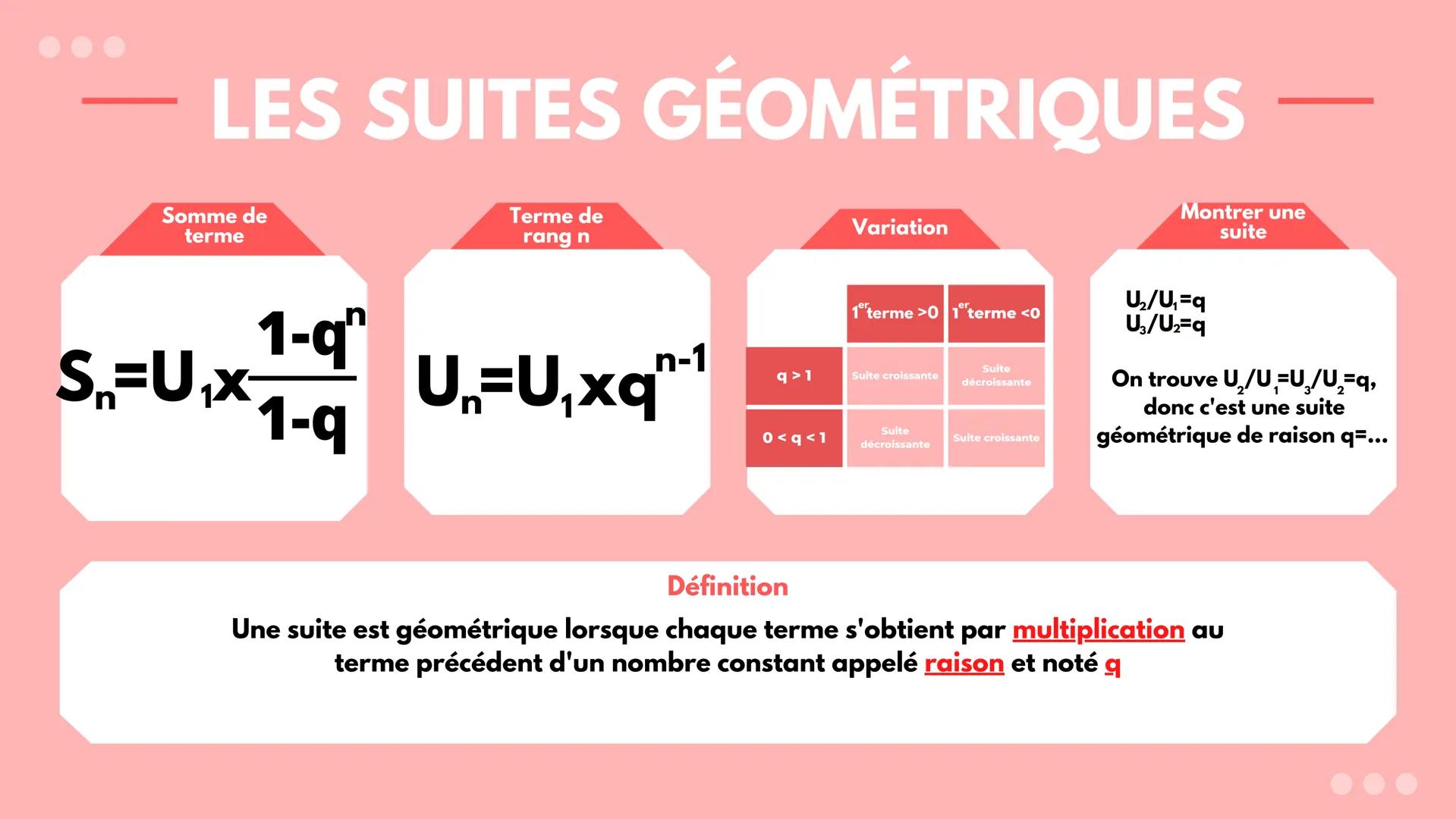
Tu vas voir, les suites géométriques c'est plus simple que ça en a l'air ! Une suite est géométrique quand tu obtiens chaque terme en multipliant le précédent par un nombre constant qu'on appelle la raison q.
Pour reconnaître une suite géométrique, c'est facile : tu calcules U₂/U₁ et U₃/U₂. Si tu obtiens le même résultat, bingo ! C'est une suite géométrique et ce résultat est ta raison q.
Le terme de rang n se calcule avec la formule : Uₙ = U₁ × qⁿ⁻¹. Cette formule te permet de trouver n'importe quel terme sans calculer tous ceux d'avant.
Astuce pratique : Pour la somme des n premiers termes, utilise Sₙ = U₁ × 1−qn/1−q. Cette formule est ton meilleur ami pour les exercices !
La variation de ta suite dépend du signe du premier terme et de la valeur de q. Si le premier terme est positif et q > 1, ta suite sera croissante. Si 0 < q < 1, elle sera décroissante. Avec un premier terme négatif, c'est l'inverse !