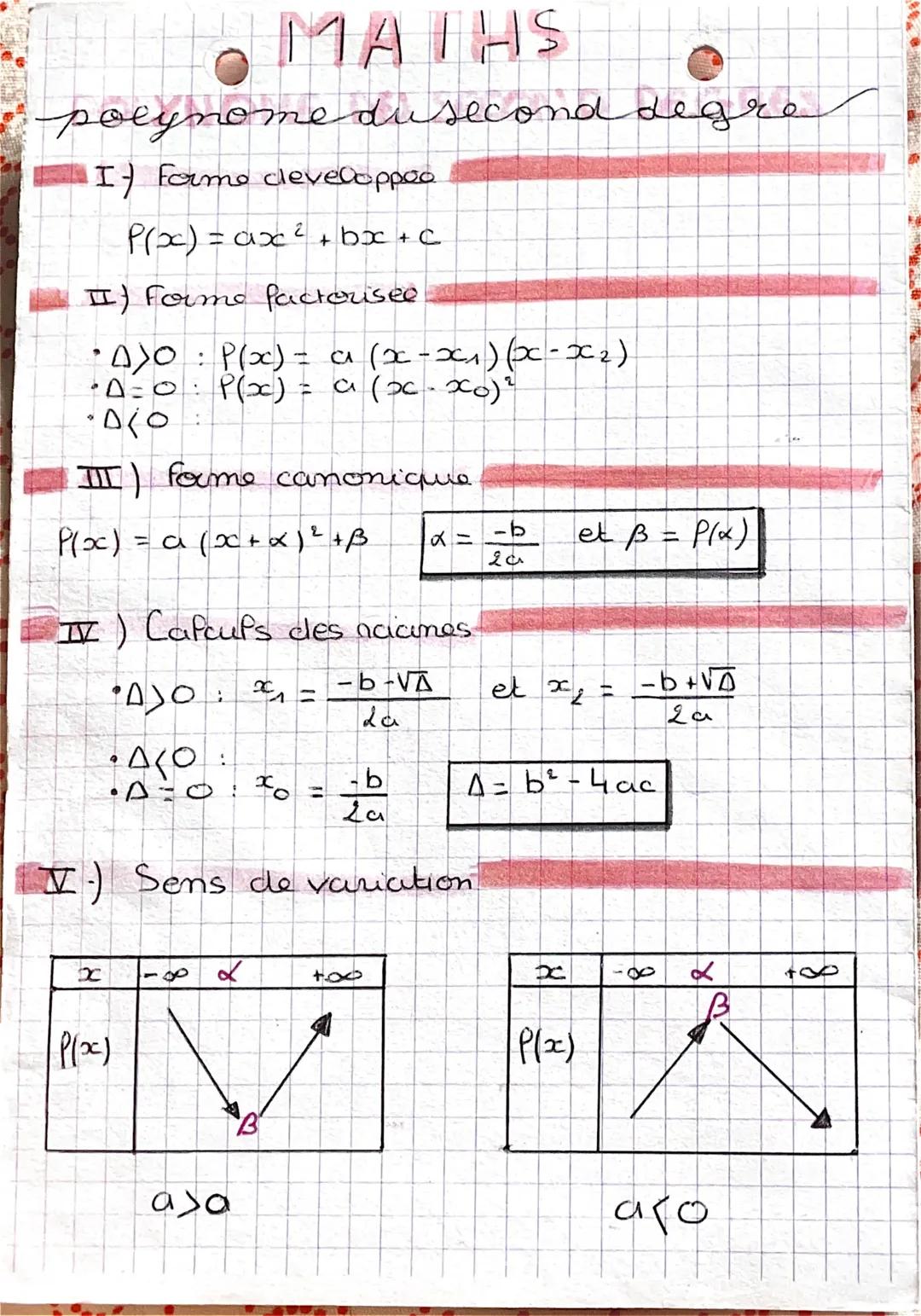
Application de la dérivation
Étudier les variations d'une fonction avec la dérivée, c'est un jeu d'enfant une fois que tu connais la méthode ! Tout repose sur le signe de f'(x) : positif = croissante, négatif = décroissante.
Ta méthode en trois étapes : d'abord tu calcules la dérivée, puis tu étudies son signe, et enfin tu dresses ton tableau de variations. Dans le tableau, n'oublie pas d'utiliser les flèches ↗ pour croissant et ↘ pour décroissant.
Pour un polynôme du second degré, c'est encore plus direct ! Sa dérivée est une fonction affine, donc super facile à étudier. Le changement de signe se fait toujours au point α = -b/2a.
💡 Rappel : f'(x) = 0 ne signifie pas que f est constante, mais qu'il y a un extremum !