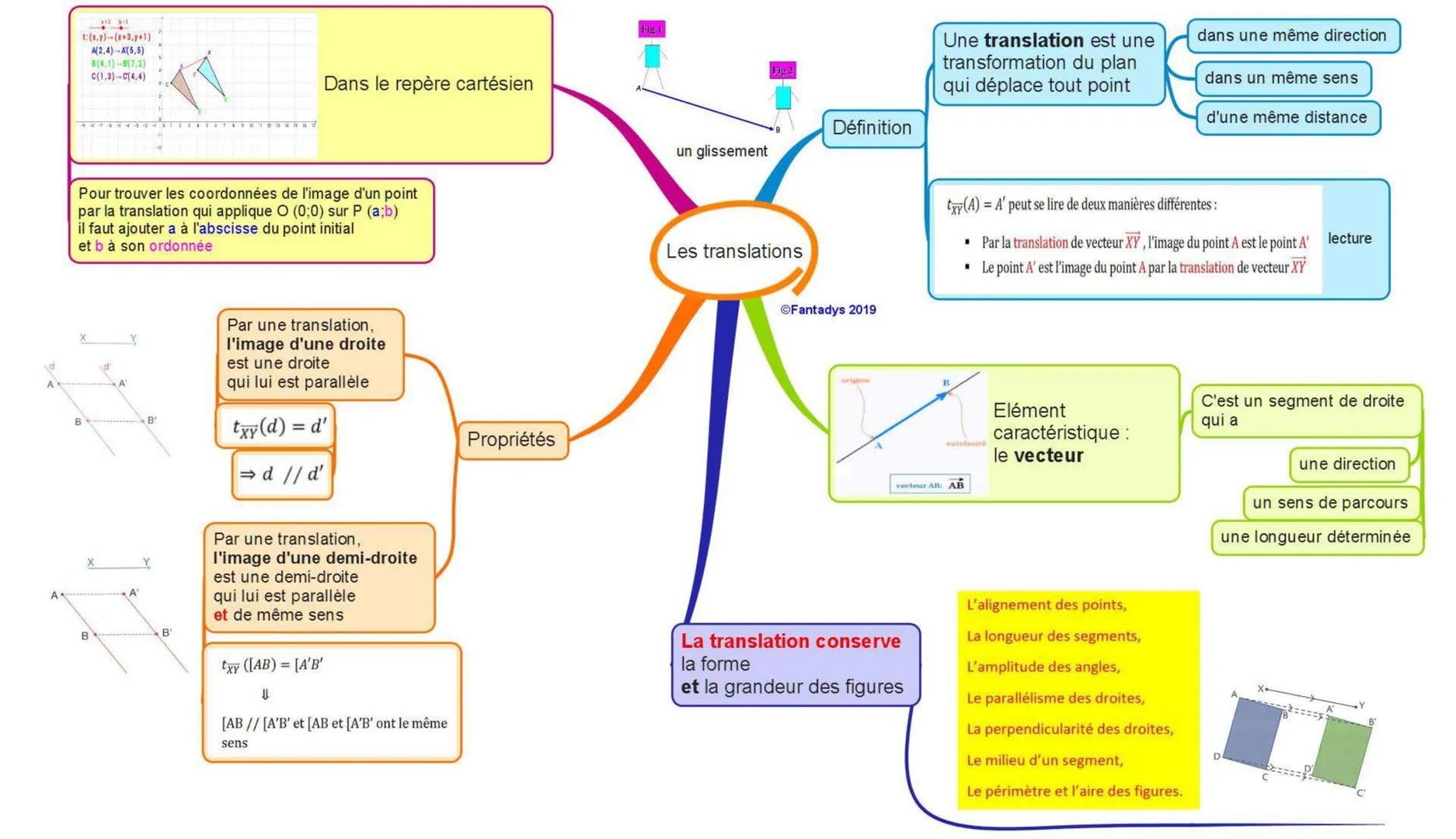
Les translations : un glissement parfait

Imagine que tu fais glisser ton téléphone sur une table - c'est exactement ce qu'est une translation ! Cette transformation déplace chaque point du plan dans la même direction, le même sens et sur la même distance.

L'élément magique qui caractérise une translation, c'est le vecteur. Un vecteur, c'est comme une flèche qui indique trois choses : où aller (direction), dans quel sens, et combien de cases parcourir (longueur).

Pour trouver les coordonnées de l'image d'un point, c'est super simple ! Si tu veux appliquer la translation qui amène O(0;0) vers P(a;b), tu ajoutes a à l'abscisse et b à l'ordonnée de ton point de départ.

💡 Astuce pratique : Quand tu vois A(2,4) → A'(5,5), tu peux lire ça de deux façons : "l'image de A par la translation" ou "A' est obtenu en appliquant la translation à A".

Ce que la translation préserve comme par magie

Voici la partie géniale : une translation conserve tout ! La forme des figures reste identique, les longueurs des segments ne changent pas, et les angles gardent la même amplitude.

Les droites parallèles restent parallèles, les droites perpendiculaires gardent leur angle droit. Même le milieu d'un segment reste au milieu de son image !

En gros, si tu traduis un triangle, tu obtiens un triangle parfaitement identique, juste déplacé. Le périmètre et l'aire ? Ils restent exactement les mêmes.